Diberikan titik R(1,4) di luar lingkaran L≡x2+y2−2y=1. Tentukan: d. Lukiskan sketsa grafiknya.

Pertanyaan

Diberikan titik $\mathrm R\left(1,4\right)$ di luar lingkaran $L\equiv x^2+y^2-2y=1$ . Tentukan:

d. Lukiskan sketsa grafiknya.

E. Lestari

Master Teacher

Mahasiswa/Alumni Universitas Sebelas Maret

Jawaban terverifikasi

Jawaban

sketsa grafiknya seperti pada gambar di atas.

Pembahasan

Ingat kembali:

Persamaan garis polar pada lingkaran $L\equiv x^2+y^2+Ax+Bx+C=0$ yang melalui titik $\left(x_1,y_1\right)$ adalah:

$x_{1\cdot}x+y_1\cdot y+\frac A2\left(x_1+x\right)+\frac B2\left(y_1+y\right)+C=0$

Persamaan garis singgung pada lingkaran $L\equiv x^2+y^2+Ax+Bx+C=0$ pada titik $\left(x_1,y_1\right)$ adalah:

$x_{1\cdot}x+y_1\cdot y+\frac A2\left(x_1+x\right)+\frac B2\left(y_1+y\right)+C=0$

Pada soal diketahui bahwa:

$\begin{array}{rcl}x^2+y^2-2y&=&1\\x^2+y^2-2y-1&=&0\\&&{A=0,\;B=-2,\;C=-1}\end{array}$

$R\left(1,4\right)\rightarrow x_1=1,\;y_1=4$

Titik yang diberikan adalah $\mathrm R\left(1,4\right)$ yang berada di luar lingkaran, sehingga diperoleh persamaan garis polarnya,

$table attributes columnalign right center left columnspacing 0px end attributes row cell x subscript 1 times end subscript x plus y subscript 1 times y plus A over 2 open parentheses x subscript 1 plus x close parentheses plus B over 2 open parentheses y subscript 1 plus y close parentheses plus C end cell equals 0 row cell 1 times x plus 4 times y plus 0 over 2 open parentheses 1 plus x close parentheses plus fraction numerator negative 2 over denominator 2 end fraction open parentheses 4 plus y close parentheses plus open parentheses negative 1 close parentheses end cell equals 0 row cell x plus 4 y minus 1 open parentheses 4 plus y close parentheses minus 1 end cell equals 0 row cell x plus 4 y minus 4 minus y minus 1 end cell equals 0 row cell x plus 3 y minus 5 end cell equals 0 row x equals cell negative 3 y plus 5 end cell end table$

Selanjutnya menentukan titik potong lingkaran dan garis polar, dengan cara mensubstitusi nilai $x$ ke persamaan lingkaran:

$\begin{array}{rcl}x^2+y^2-2y-1&=&0\\\left(-3y+5\right)^2+y^2-2y-1&=&0\\9y^2-30y+25+y^2-2y-1&=&0\\10y^2-32y+24&=&0\\5y^2-16y+12&=&0\\\left(5y-6\right)\left(y-2\right)&=&0\\&&{y=\frac65\;\text{atau}\;y=2}\end{array}$

Substitusi nilai $y$ ke persamaan polar

$\begin{array}{cc}y=\frac65\rightarrow&\begin{array}{rcl}x&=&-3y+5\end{array}\\&\begin{array}{rcl}x&=&-3\left(\frac65\right)+5\end{array}\\&\begin{array}{rcl}x&=&-\frac{18}5+5\end{array}\\&x=\frac75\\&\\y=2&\begin{array}{rcl}x&=&-3x+5\end{array}\\&\begin{array}{rcl}x&=&-3\left(2\right)+5\end{array}\\&x=-6+5\\&x=-1\end{array}$

Didapat titik singgung lingkaran dengan garis polar adalah $\mathrm A\left(\frac75,\;\frac65\right)\;\mathrm{dan}\;\mathrm B\left(-1,2\right)$ .

Diperoleh persamaan garis singgung lingkarannya:

Untuk titik $\mathrm A\left(\frac75,\;\frac65\right)$

$table attributes columnalign right center left columnspacing 0px end attributes row cell x subscript 1 times end subscript x plus y subscript 1 times y plus A over 2 open parentheses x subscript 1 plus x close parentheses plus B over 2 open parentheses y subscript 1 plus y close parentheses plus C end cell equals 0 row cell 7 over 5 x plus 6 over 5 times y plus 0 over 2 open parentheses 7 over 5 plus x close parentheses plus fraction numerator negative 2 over denominator 2 end fraction open parentheses 6 over 5 plus y close parentheses plus open parentheses negative 1 close parentheses end cell equals 0 row cell 7 over 5 x plus 6 over 5 times y minus 6 over 5 minus y minus 1 end cell equals 0 row cell 7 x plus 6 y minus 6 minus 5 y minus 5 end cell equals 0 row cell 7 x plus y minus 11 end cell equals 0 end table$

Untuk titik $\mathrm B\left(-1,2\right)$ .

$table attributes columnalign right center left columnspacing 0px end attributes row cell x subscript 1 times end subscript x plus y subscript 1 times y plus A over 2 open parentheses x subscript 1 plus x close parentheses plus B over 2 open parentheses y subscript 1 plus y close parentheses plus C end cell equals 0 row cell open parentheses negative 1 close parentheses x plus 2 times y plus 0 over 2 open parentheses open parentheses negative 1 close parentheses plus x close parentheses plus fraction numerator negative 2 over denominator 2 end fraction open parentheses 2 plus y close parentheses plus open parentheses negative 1 close parentheses end cell equals 0 row cell negative x plus 2 y minus 2 minus y minus 1 end cell equals 0 row cell negative x plus y minus 3 end cell equals 0 end table$

Akan ditentukan sketsa grafiknya:

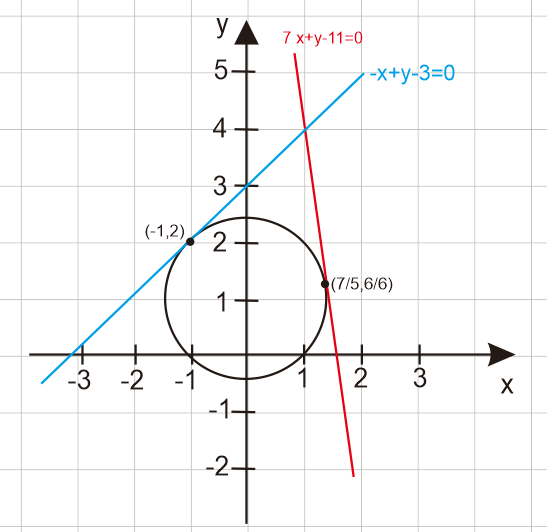
Dengan demikian, sketsa grafiknya seperti pada gambar di atas.

455

0.0 (0 rating)

Pertanyaan serupa

8a. Tentukan titik potong lingkaran L≡x2+y2−2x−4y−3=0 terhadap sumbu X. 8b. Tentukan persamaan garis singgung di titik potong tersebut.

715

0.0

Jawaban terverifikasi

Garis x=5 memotong lingkaran x2+y2−4x−6y−12=0 di dua titik. b. Tentukan persamaan garis singgung yang melalui masing-masing dua titik tersebut.

136

0.0

Jawaban terverifikasi

Tunjukkan bahwa garis singgung pada lingkaran L≡x2+y2−2x−4y−15=0 di titik-titik yang merupakan titik potong antara lingkaran tersebut dengan sumbu X akan berpotongan di titik (1, −8).

263

0.0

Jawaban terverifikasi

Diberikan titik R(1,4) di luar lingkaran L≡x2+y2−2y=1. Tentukan: c. Persamaan garis singgung yang melalui titik A dan titik B.

319

4.0

Jawaban terverifikasi

Garis yang melalui P(1, 2) menyinggung lingkaran x2+y2−14x+12y+49=0 di titik M. Jarak PM sama dengan ....

585

5.0

Jawaban terverifikasi