Iklan
Pertanyaan
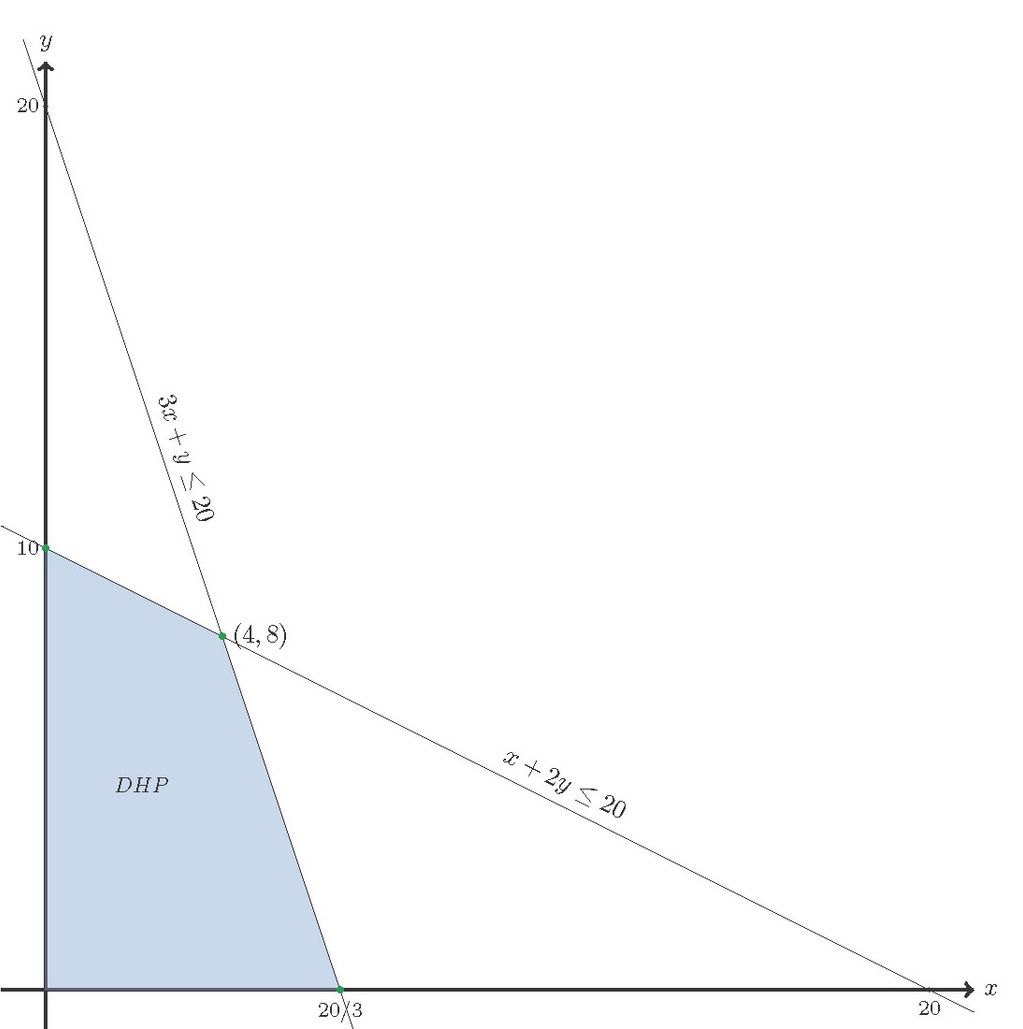
Dengan persediaan kain polos 20 m dan kain bergaris 10 m , seorang penjahit akan membuat pakaian jadi. Model Imemerlukan 1 m kain polos dan 1 , 5 m kain bergaris. Model II memerlukan 2 m kain polos dan 0 , 5 m kain bergaris. Jika keuntungan untuk model I Rp 15.000 , 00 dan model II Rp 25.000 , 00 , maka keuntungan maksimum dicapai bila model I dan II masing-masing berjumlah ...
Dengan persediaan kain polos dan kain bergaris , seorang penjahit akan membuat pakaian jadi. Model I memerlukan kain polos dan kain bergaris. Model II memerlukan kain polos dan kain bergaris. Jika keuntungan untuk model I dan model II , maka keuntungan maksimum dicapai bila model I dan II masing-masing berjumlah ...
Iklan
NP
N. Puspita
Master Teacher
Jawaban terverifikasi
2
5.0 (1 rating)
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia