Pertanyaan

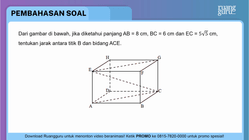
Dari gambar di bawah, jika diketahui panjang AB = 8 cm , BC = 6 cm dan EC = 5 5 cm , tentukan jarak antara titik B dan bidang ACE.

Dari gambar di bawah, jika diketahui panjang $AB = 8 cm$ , $BC = 6 cm$ dan $EC = 55 cm$ , tentukan jarak antara titik B dan bidang ACE.

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

N. Puspita

Master Teacher

Jawaban terverifikasi

Jawaban

jarak titik B ke bidang ACE adalah .

jarak titik B ke bidang ACE adalah 4 comma 8 space cm

Pembahasan

Ingat! Jarak titik ke bidang adalah lintasan terpendek yang menghubungkan titik dan tegak lurus terhadap bidang. Pada segitiga siku-siku berlaku teorema Pythagoras dengan adalah sisi siku-siku dan sisi miring. Jika dalam suatu segitiga terdapat 2 garis yang dapat dijadikan tinggi ( dan ) dan 2 garis yang dapat dijadikan alas ( dan ), maka berlaku . Perhatikan segitiga ACE siku-siku di A, sehingga berlaku teorema Pythagoras sebagai berikut: Jarak titik B ke bidang ACE adalah BP. Perhatikan segitiga ABC memiliki 2 tinggi dan 2 alas sehingga berlaku rumuskesamaan luas segitiga sebagai berikut: Jadi, jarak titik B ke bidang ACE adalah .

Ingat!

Jarak titik ke bidang adalah lintasan terpendek yang menghubungkan titik dan tegak lurus terhadap bidang.
Pada segitiga siku-siku berlaku teorema Pythagoras dengan adalah sisi siku-siku dan sisi miring.
Jika dalam suatu segitiga terdapat 2 garis yang dapat dijadikan tinggi ( dan ) dan 2 garis yang dapat dijadikan alas ( dan ), maka berlaku $t subscript 2 equals fraction numerator a subscript 1 cross times t subscript 1 over denominator a subscript 2 end fraction$ .

Perhatikan segitiga ACE siku-siku di A, sehingga berlaku teorema Pythagoras sebagai berikut:

Jarak titik B ke bidang ACE adalah BP. Perhatikan segitiga ABC memiliki 2 tinggi dan 2 alas sehingga berlaku rumus kesamaan luas segitiga sebagai berikut:

$table attributes columnalign right center left columnspacing 0px end attributes row BP equals cell fraction numerator AB cross times BC over denominator AC end fraction end cell row blank equals cell fraction numerator 8 cross times 6 over denominator 10 end fraction end cell row blank equals cell 48 over 10 end cell row blank equals cell 4 comma 8 space cm end cell end table$

Jadi, jarak titik B ke bidang ACE adalah .

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.7 (70 rating)

Ainun Madina

Pembahasan lengkap banget Makasih ❤️ Mudah dimengerti Ini yang aku cari! Bantu banget

Samuel Tito T

Pembahasan lengkap banget Makasih ❤️

M. Luthfiansyah Khadafi

Pembahasan lengkap banget

Nadya Eka

Makasih ❤️ Ini yang aku cari! Bantu banget Mudah dimengerti Pembahasan lengkap banget

Suci Srirahayu

Ini yang aku cari!

Pertanyaan serupa

Diketahui kubus K OP I . C U R A dengan panjang rusuk 9cm . Jika S proyeksi titik P pada bidang K U A , jarak titik K ke titik sama dengan ...

4.0

Jawaban terverifikasi

Diketahui limas beraturan T.ABCD dengan AB = 8 cm dan TA = 12 cm . Hitunglah jarak titik T ke bidang ABCD.

168

4.7

Jawaban terverifikasi

Diketahui kubus ABCD . EFGH dengan panjang rusuk 10 cm . Titik P dan Q masing-masing terletak di tengah-tengah rusuk AB dan AF . Jarak titik C ke bidang DPQH adalah ....

4.8

Jawaban terverifikasi

Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm . Titik P pada perpanjangan CD sehingga CD : DP = 3 : 1 . Jarak antara titik P ke bidang ACGE adalah ... cm .

4.8

Jawaban terverifikasi

Dalam kubus ABCD.EFGH titik S adalah titik tengah sisi CD dan P adalah titik tengah diagonal ruang BH. Tentukan perbandingan volum limas P.BCS dan volum kubus ABCD.EFGH.

4.8

Jawaban terverifikasi