Daerah yang memenuhi sistem pertidaksamaan : x + y ≤ 4 ; 2 x − y ≤ 4 ; 2 y − x ≤ 4 ; x ≥ 0 ; y ≥ 0 , adalah...

Pembahasan

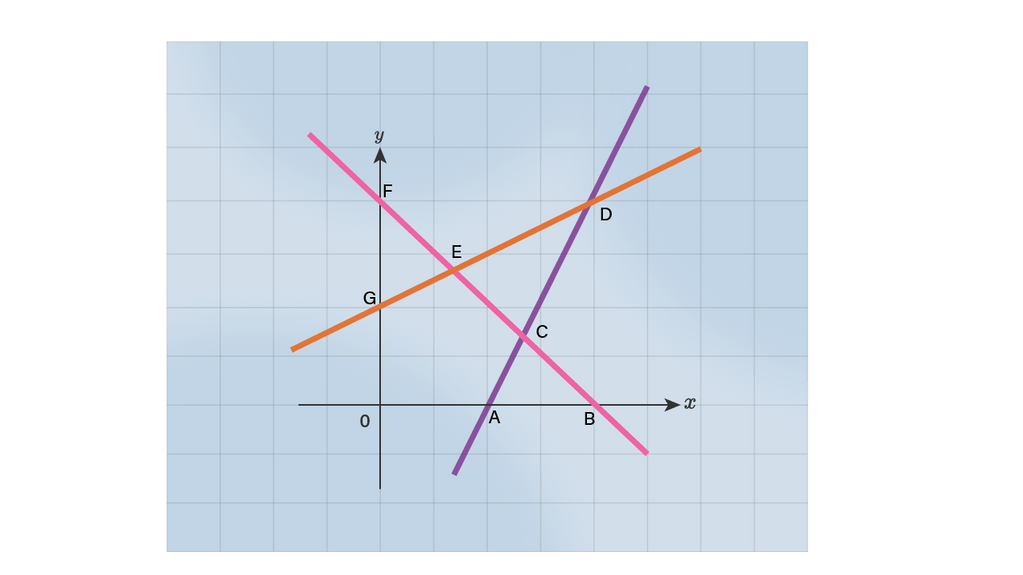
1. Tentukan persamaan masing-masing garis: x + y ≤ 4 Ubah pertidaksamaan menjadi sebuah persamaan x + y = 4 Jika x = 0 maka y = 4 Jika y = 0 maka x = 4 Di dapatkan dua titik yaitu ( 0 , 4 ) dan ( 4 , 0 ) , mengartikan bahwa garis melewati titik ( 0 , 4 ) dan ( 4 , 0 ) . 2 x − y ≤ 4 ; Ubah pertidaksamaan menjadi sebuah persamaan 2 x − y = 4 Jika x = 0 maka y = − 4 Jika y = 0 maka x = 2 Di dapatkan dua titik yaitu ( 0 , − 4 ) dan ( 2 , 0 ) , mengartikan bahwa garis melewati titik ( 0 , − 4 ) dan ( 2 , 0 ) . 2 y − x ≤ 4 ; Jika x = 0 maka y = 2 Jika y = 0 maka x = − 4 Di dapatkan dua titik yaitu ( 0 , 2 ) dan ( − 4 , 0 ) , mengartikan bahwa garis melewati titik ( 0 , 2 ) dan ( − 4 , 0 ) . Sehingga diperoleh kesesuaian antara garis dan persamaannya adalah sebagai berikut. 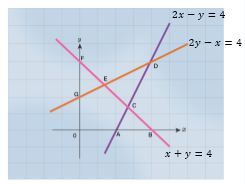2. Lakukan uji titik dan tentukan daerah penyelesaian(Misal titik uji ( 0 , 0 ) ) x + y ≤ 4 x + y 0 + 0 0 ​ ≤ ≤ ≤ ​ 4 4 4 ( benar ) ​ Karena benar bahwa 0 ≤ 4 , maka daerah yang memuat titik ( 0 , 0 ) merupakan daerah penyelesaian dari x + y ≤ 4 . 2 x − y ≤ 4 2 x − y 2 ⋅ 0 − 0 0 ​ ≤ ≤ ≤ ​ 4 4 4 ( benar ) ​ Karena benar bahwa 0 ≤ 4 , maka daerah yang memuat titik ( 0 , 0 ) merupakan daerah penyelesaian dari 2 x − y ≤ 4 . 2 y − x ≤ 4 2 y − x 2 ⋅ 0 − 0 0 ​ ≤ ≤ ≤ ​ 4 4 4 ( benar ) ​ Karena benar bahwa 0 ≤ 4 , maka daerah yang memuat titik ( 0 , 0 ) merupakan daerah penyelesaian dari 2 y − x ≤ 4 . x ≥ 0 ; dan y ≥ 0 karena tanda lebihdari maka daerah penyelesaian beradadi kanansumbu-Y dan di atas sumbu-X. 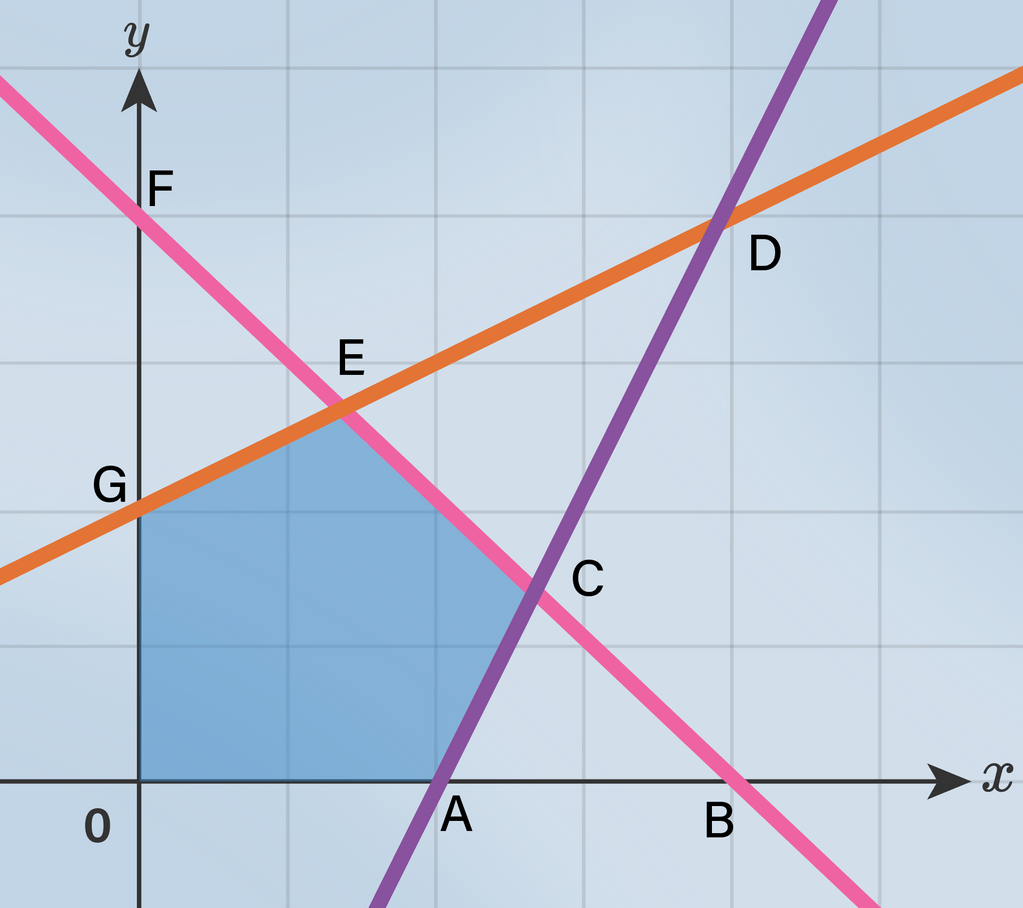Daerah himpunan penyelesaian dapat digambarkan sebagai berikut : Jadi, daerah yang memenuhi sistem pertidaksamaan : x + y ≤ 4 ; 2 x − y ≤ 4 ; 2 y − x ≤ 4 ; x ≥ 0 ; y ≥ 0 , adalah OACEG . Oleh karena itu, jawaban yang benar adalah A.