Ingat kembali rumus untuk menentukan persamaan garis lurus dari dua titik yang diketahui yaitu.

Untuk menentukan model matematika atau sistem pertidaksamaan dari daerah yang diarsir dapat menggunakan langkah-langkah berikut.
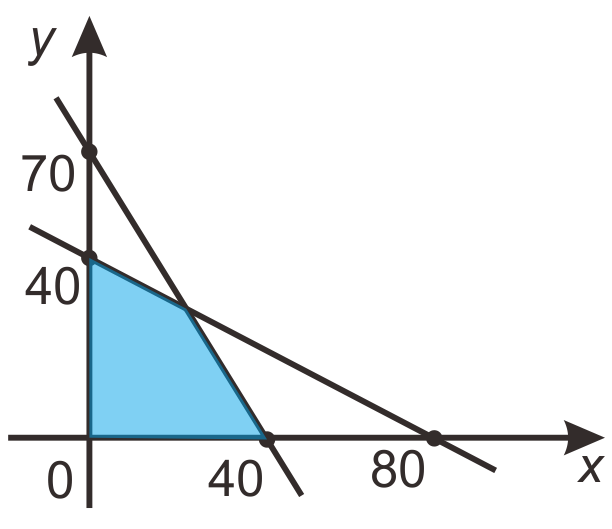
Pada gambar tersebut terdapat empat garis yaitu:
- Garis I yang melalui titik
 dan
dan  .
.
- Garis II yang melalui titik
 dan
dan  .
.
- Garis III yaitu sumbu
 .
.
- Garis IV yaitu sumbu
 .
.
Kemudian tentukan persamaan garis tersebut.
*Persamaan garis I yang melalui titik  dan
dan  .
.

Diperoleh persamaan garis I adalah  .
.
*Persamaan garis II yang melalui titik  dan
dan  .
.

Diperoleh persamaan garis II adalah  .
.
Persamaan garis III yaitu sumbu  yaitu
yaitu  .
.
Persamaan garis IV yaitu sumbu  yaitu
yaitu  .
.
*Kemudian tentukan tanda ketaksamaan masing-masing persamaan.
Ambil satu titik uji yang ada di daerah himpunan penyelesaian, pada gambar diambil titik  agar mudah menghitungnya, kemudian substitusikan ke persamaan garis kemudian tentukan tanda ketaksamaan dari hasil yang diperoleh.
agar mudah menghitungnya, kemudian substitusikan ke persamaan garis kemudian tentukan tanda ketaksamaan dari hasil yang diperoleh.
Garis I  .
.

Tanda ketaksamaan persamaan garis I adalah  , sehingga diperoleh pertidaksamaan garis I adalah
, sehingga diperoleh pertidaksamaan garis I adalah  .
.
Garis II  .
.

Tanda ketaksamaan persamaan garis II adalah  , sehingga diperoleh pertidaksamaan garis II adalah
, sehingga diperoleh pertidaksamaan garis II adalah  .
.
Garis III  .
.
Karena daerah himpunan penyelesaian berada di sebelah kanan garis  , maka diperoleh pertidaksamaannya adalah
, maka diperoleh pertidaksamaannya adalah  .
.
Garis IV  .
.
Karena daerah himpunan penyelesaian berada di sebelah atas garis  , maka diperoleh pertidaksamaannya adalah
, maka diperoleh pertidaksamaannya adalah  .
.
Jadi, diperoleh model matematika atau sistem pertidaksamaan dari gambar tersebut adalah  ,
,  ,
,  , dan
, dan  .
.