Pertanyaan

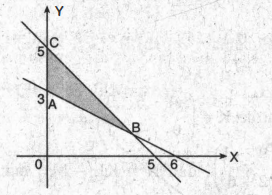
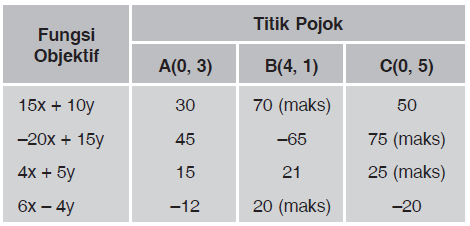
Daerah yang diarsir berikut ini merupakan daerah penyelesaian suatu sistem pertidaksamilan linear. Diberikan bentuk-bentuk fungsi objektif berikut ini. (i) 15 x + 10 y (iii) 4 x + 5 y (ii) − 20 x + 15 y (iv) 6 x − 4 y Di antara bentuk-bentuk tersebut yang'mencapai maksimum di titik C adalah ....

Daerah yang diarsir berikut ini merupakan daerah penyelesaian suatu sistem pertidaksamilan linear.

Diberikan bentuk-bentuk fungsi objektif berikut ini.
(i) $15 x + 10 y$ (iii) $4 x + 5 y$
(ii) $- 20 x + 15 y$ (iv) $6 x - 4 y$
Di antara bentuk-bentuk tersebut yang'mencapai maksimum di titik C adalah ....

(i), (ii), dan (iii)
(i) dan (iii)
(ii) dan (iii)
(iii) saja
(iv) saja

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

L. Sibuea

Master Teacher

Mahasiswa/Alumni Universitas Riau

Jawaban terverifikasi

Pembahasan

Daerah penyelesaian tersebut memilikilima titik pojok, yaitu A, B, danC. Koordinat titik A adalah dan titik C adalah . Titik B adalah perpotongan antara garis AB dan BC. Garis AB melalui titik sehingga persamaan garisnya adalah . Garis BC melalui titik sehingga persamaan garisnya adalah . Koordinat titik B diperoleh dengan mengeliminasi persamaan garis AB dan BC sehingga koordinat titik B adalah . Substitusikan masing-masing titik pojok ke fungsi obyektif. Dari tabel terlihat bahwa fungsi obyektif yang mencapai maksimum di titik C adalah . Jadi, jawaban yang tepat adalah C

Daerah penyelesaian tersebut memiliki lima titik pojok, yaitu A, B, dan C.

Koordinat titik A adalah dan titik C adalah .

Titik B adalah perpotongan antara garis AB dan BC. Garis AB melalui titik sehingga persamaan garisnya adalah . Garis BC melalui titik sehingga persamaan garisnya adalah . Koordinat titik B diperoleh dengan mengeliminasi persamaan garis AB dan BC sehingga koordinat titik B adalah .

Substitusikan masing-masing titik pojok ke fungsi obyektif.

Dari tabel terlihat bahwa fungsi obyektif yang mencapai maksimum di titik C adalah .

Jadi, jawaban yang tepat adalah C

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

5.0 (1 rating)

Pertanyaan serupa

Perhatikan gambar berikut. Nilai minimum fungsi objektif f ( x , y ) = y − 2 x dicapai di titik ....

5.0

Jawaban terverifikasi

Jikafungsi f ( x , y ) = 3 x − 2 y dengan syarat x − y ≥ − 2 , dan x + y ≤ 4 maka ....

4.5

Jawaban terverifikasi

Nilai maksimum dan minimum dari SPtLDV f ( x , y ) = 4 x + 3 y dengan syarat x ≥ 0 , y ≥ 0 , x + y ≥ 3 dan 2 x + y ≥ 4 adalah ...

5.0

Jawaban terverifikasi

Seorang pembuat roti setiap hari membuat dua jenis roti yaitu roti A dan roti B. Banyak roti yang dibuat tidak kurang dari 50 cetak per hari. Banyak roti A yang dibuat tidak kurang dari 10 cetakper ha...

5.0

Jawaban terverifikasi

Sebuah pabrik mempunyai dua jenis mesin untuk memproduksi paling sedikit 220 unit barang per hari. Mesin I mampu menghasilkan 10 unit barang per jam. Mesin II mampu menghasilkan 20 unit barang per jam...

5.0

Jawaban terverifikasi