Iklan
Pertanyaan
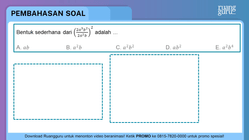
Bentuk sederhana dari ( 2 a 2 b 2 a 3 b 2 ) 2 adalah ....
Bentuk sederhana dari adalah ....
Iklan
SN
S. Nur
Master Teacher
Jawaban terverifikasi
2
3.6 (9 rating)
ek
erameita kristina
Makasih ❤️
RA
Rian Ahmad
Makasih ❤️
Za
Zulfa az Zahra
Bantu banget Pembahasan lengkap banget Ini yang aku cari! Mudah dimengerti Makasih ❤️
R
Radzuan
membantu meningkatkan
PT
Prizema Talita
Jawaban tidak sesuai
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2025 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia