Iklan
Pertanyaan
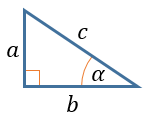
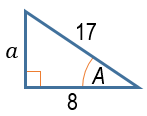
2. Jika cos A = 17 8 dan A sudut lancip,maka nilai dari sin 2 A adalah....
2. Jika dan sudut lancip, maka nilai dari adalah ....
Iklan
IR
I. Ridha
Master Teacher
Mahasiswa/Alumni Universitas Negeri Surabaya
Jawaban terverifikasi
2
4.7 (19 rating)
Fz
Fathimatuz zahra
Mudah dimengerti
F
Farassha
Mudah dimengerti Makasih ❤️
P
Pelsa
Ini yang aku cari! Bantu banget Makasih ❤️
IK
I Kmg Art
Makasih ❤️
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2025 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia