Diana R
14 Agustus 2025 03:50
Iklan
Diana R
14 Agustus 2025 03:50
Pertanyaan
1. Diketahui f(x)=2x-4\5-x, x≠5 dan g(x)=3x+7, Tentukan: a) f pangkat min 1 (x) b) g(x) c) (gof) (x) d) (gof) pangkat min 1 (x) e) (f pangkat min 1 o g pangkat min 1) (x) 2. Tentukan invers fungsi a) f(x)= 5-4x\7x-3 b) g(x)= 1\2x-6 c) g(x)= 3 √x-2
7
3
Iklan
E. Nur
14 Agustus 2025 09:39
<p>Pembahsan 1a dan 1b pada gambar terlampir</p>
Pembahsan 1a dan 1b pada gambar terlampir
· 5.0 (3)
Din A
21 Agustus 2025 01:12
gimana caranya
Iklan
Hayykkpapelsl H
14 Agustus 2025 05:27
<p>oke</p>
oke
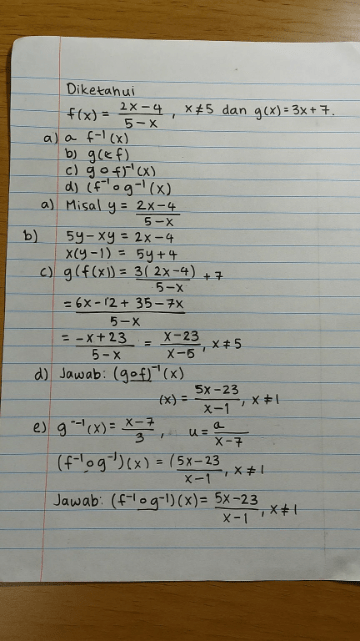
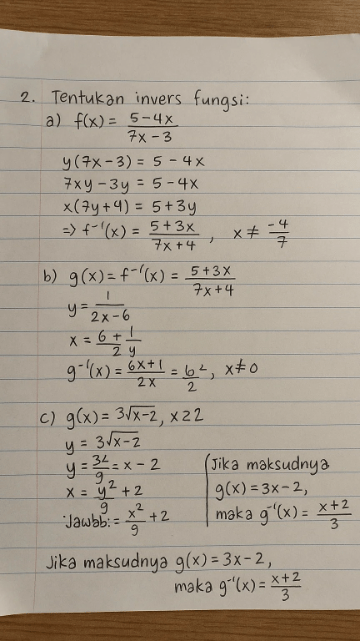
· 4.8 (4)
Muhammad A
14 Agustus 2025 10:11
<p>124,54</p>
124,54
· 1.0 (2)
Irmansyah J
17 Agustus 2025 17:43
Ini jawaban gua Soal 1: Diketahui f(x) = \frac{2x-4}{5-x}, x \neq 5 dan g(x) = 3x+7. Tentukan: - a) f^{-1}(x) - b) g(x) - c) (g \circ f)(x) - d) (g \circ f)^{-1}(x) - e) (f^{-1} \circ g^{-1})(x) Penyelesaian: a) Mencari f^{-1}(x): - Misalkan y = \frac{2x-4}{5-x} - y(5-x) = 2x-4 - 5y - xy = 2x - 4 - 5y + 4 = 2x + xy - 5y + 4 = x(2+y) - x = \frac{5y+4}{2+y} - Jadi, f^{-1}(x) = \frac{5x+4}{x+2} b) g(x) = 3x + 7 (sudah diketahui) c) Mencari (g \circ f)(x) = g(f(x)): - g(f(x)) = g\left(\frac{2x-4}{5-x}\right) - g(f(x)) = 3\left(\frac{2x-4}{5-x}\right) + 7 - g(f(x)) = \frac{6x-12}{5-x} + 7 - g(f(x)) = \frac{6x-12 + 7(5-x)}{5-x} - g(f(x)) = \frac{6x-12 + 35 - 7x}{5-x} - g(f(x)) = \frac{-x + 23}{5-x} d) Mencari (g \circ f)^{-1}(x): - Misalkan y = \frac{-x+23}{5-x} - y(5-x) = -x + 23 - 5y - xy = -x + 23 - 5y - 23 = xy - x - 5y - 23 = x(y-1) - x = \frac{5y-23}{y-1} - Jadi, (g \circ f)^{-1}(x) = \frac{5x-23}{x-1} e) Mencari (f^{-1} \circ g^{-1})(x): - Pertama, cari g^{-1}(x): - Misalkan y = 3x + 7 - y - 7 = 3x - x = \frac{y-7}{3} - Jadi, g^{-1}(x) = \frac{x-7}{3} - Kemudian, cari (f^{-1} \circ g^{-1})(x) = f^{-1}(g^{-1}(x)): - f^{-1}(g^{-1}(x)) = f^{-1}\left(\frac{x-7}{3}\right) - f^{-1}(g^{-1}(x)) = \frac{5\left(\frac{x-7}{3}\right) + 4}{\left(\frac{x-7}{3}\right) + 2} - f^{-1}(g^{-1}(x)) = \frac{\frac{5x-35}{3} + 4}{\frac{x-7}{3} + 2} - f^{-1}(g^{-1}(x)) = \frac{\frac{5x-35+12}{3}}{\frac{x-7+6}{3}} - f^{-1}(g^{-1}(x)) = \frac{5x - 23}{x - 1} Soal 2: Tentukan invers fungsi: - a) f(x) = 5 - 4x^{7x-3} - b) g(x) = \frac{1}{2x - 6} - c) g(x) = 3\sqrt{x} - 2 Penyelesaian: a) f(x) = 5 - 4x^{7x-3} (Soal ini sepertinya kurang jelas, terutama pada bagian pangkat. Cici akan asumsikan soalnya adalah f(x) = 5 - 4x) - y = 5 - 4x - 4x = 5 - y - x = \frac{5-y}{4} - Jadi, f^{-1}(x) = \frac{5-x}{4} b) g(x) = \frac{1}{2x - 6} - y = \frac{1}{2x - 6} - 2x - 6 = \frac{1}{y} - 2x = \frac{1}{y} + 6 - x = \frac{1}{2y} + 3 - Jadi, g^{-1}(x) = \frac{1}{2x} + 3 c) g(x) = 3\sqrt{x} - 2 - y = 3\sqrt{x} - 2 - y + 2 = 3\sqrt{x} - \frac{y+2}{3} = \sqrt{x} - x = \left(\frac{y+2}{3}\right)^2 - Jadi, g^{-1}(x) = \left(\frac{x+2}{3}\right)^2 Semoga penjelasan ini membantu!
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



