Pertanyaan

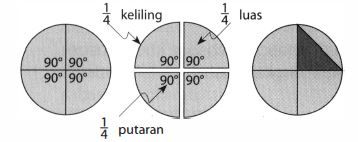
Untuk membagi lingkaran sama besar, paling mudah dengan membagi melalui pusat lingkaran. Jika lingkaran belum dipotong, maka besar sudut adalah 1 putaran atau 36 0 ∘ . Jika lingkaran ingin dibagi menjadi empat bagian sama besar, maka sudut pusat lingkaran tersebut dibagi empat, masing-masing sebesar 9 0 ∘ . e. Bandingkan ukuran keliling lingkaran dengan panjang sisi miring segitiga.

Untuk membagi lingkaran sama besar, paling mudah dengan membagi melalui pusat lingkaran. Jika lingkaran belum dipotong, maka besar sudut adalah $1 putaran atau 36 0^{\circ}$ . Jika lingkaran ingin dibagi menjadi empat bagian sama besar, maka sudut pusat lingkaran tersebut dibagi empat, masing-masing sebesar $9 0^{\circ}$ .

e. Bandingkan ukuran keliling lingkaran dengan panjang sisi miring segitiga.

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

S. Dwi

Master Teacher

Jawaban terverifikasi

Jawaban

perbandingan ukuran keliling lingkaran dengan panjang sisi miring segitiga adalah 2 π : 2 .

perbandingan ukuran keliling lingkaran dengan panjang sisi miring segitiga adalah

2 π : 2

Pembahasan

Jawaban yang benar untuk pertanyaan tersebut adalah 2 π : 2 . Ingat! Rumus untuk menghitung keliling lingkaran adalah: K = 2 × π × r Rumus pythagoras pada segitiga siku-siku adalah: c 2 = a 2 + b 2 dengan c = sisi miring segitiga . Panjang sisi miring segitiga merupakan panjang tali busur lingkaran, sehingga dapat dicari dengan rumus pythagoras sebagai berikut: sisi miring = = = = tali busur r 2 + r 2 2 r 2 r 2 Jadi, perbandingan ukuran keliling lingkaran dengan panjang sisi miring segitiga adalah: Keliling ◯ : sisi miring △ = = 2 ⋅ π ⋅ r : r 2 2 π : 2 Dengan demikian,perbandingan ukuran keliling lingkaran dengan panjang sisi miring segitiga adalah 2 π : 2 .

Jawaban yang benar untuk pertanyaan tersebut adalah $2 π : 2$ .

Ingat!

Rumus untuk menghitung keliling lingkaran adalah:

$K = 2 \times π \times r$

Rumus pythagoras pada segitiga siku-siku adalah:

$c^{2} = a^{2} + b^{2}$

dengan $c = sisi miring segitiga$ .

Panjang sisi miring segitiga merupakan panjang tali busur lingkaran, sehingga dapat dicari dengan rumus pythagoras sebagai berikut:

$sisi miring = = = = tali busur r^{2} + r^{2} 2 r^{2} r 2$

Jadi, perbandingan ukuran keliling lingkaran dengan panjang sisi miring segitiga adalah:

$Keliling ◯ : sisi miring △ = = 2 \cdot π \cdot r : r 2 2 π : 2$

Dengan demikian, perbandingan ukuran keliling lingkaran dengan panjang sisi miring segitiga adalah $2 π : 2$ .

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

0.0 (0 rating)

Pertanyaan serupa

Kerjakan sekali lagi soal nomor 3 , jika lingkaran dibagi menjadi delapan bagian. Bandingkan hasilnya dengan lingkaran yang dibagi menjadi empat bagian.

5.0

Jawaban terverifikasi

Kerjakan sekali lagi soal nomor 3 , jika lingkaran dibagi menjadi delapan bagian. Bandingkan hasilnya dengan lingkaran yang dibagi menjadi empat bagian.

5.0

Jawaban terverifikasi

Kerjakan sekali lagi soal nomor 3, jika lingkaran dibagi menjadi enam bagian.

4.0

Jawaban terverifikasi

Perhatikan gambar berikut! Jika diketahui luas lingkaran di atas 2.464 cm 2 dan panjang busur AB 58 3 2 cm 2 , maka berapa besar ∠ ACB ! ( π = 7 22 ) . HOTS

5.0

Jawaban terverifikasi

Perhatikan gambar berikut! Jika diketahui luas lingkaran di atas 2.464 cm 2 dan panjang busur AB 58 3 2 cm 2 , maka berapa besar ∠ ACB ! ( π = 7 22 ) . HOTS

5.0

Jawaban terverifikasi