Pertanyaan

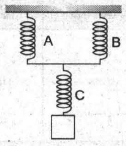
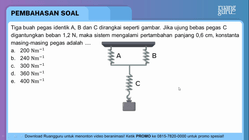
UN 2010 (Penalaran) Tiga buah pegas identik A, B dan C dirangkai seperti gambar. Jika ujung bebas pegas C digantungkan beban 1,2 N, maka sistem mengalamipertambahan panjang 0,6 cm, konstanta masing-masing pegas adalah ....

UN 2010 (Penalaran)

Tiga buah pegas identik A, B dan C dirangkai seperti gambar. Jika ujung bebas pegas C digantungkan beban 1,2 N, maka sistem mengalami pertambahan panjang 0,6 cm, konstanta masing-masing pegas adalah ....

8 dari 10 siswa nilainya naik

dengan paket belajar pilihan

Habis dalam

Klaim

N. Puspita

Master Teacher

Jawaban terverifikasi

Jawaban

jawaban yang tepat adalah C.

Pembahasan

Pada susunan rangkaiann pegas seri-paralel, maka terlebih dahulu dihitung nilai konstanta pegas pengganti sebagai berikut : Kemudian dengan menggunakan persamaan Hukum Hooke, dapat dicari : Sehingga besarkonstanta masing-masing pegas adalah . Jadi, jawaban yang tepat adalah C.

Pada susunan rangkaiann pegas seri-paralel, maka terlebih dahulu dihitung nilai konstanta pegas pengganti sebagai berikut :

$begin mathsize 14px style table attributes columnalign right center left columnspacing 0px end attributes row blank rightwards double arrow cell space 1 over k subscript p e n g g a n t i end subscript space equals space fraction numerator 1 over denominator 2 straight k end fraction space plus space 1 over straight k end cell row cell 1 over k subscript p e n g g a n t i end subscript space end cell equals cell space fraction numerator 1 space plus space 2 over denominator 2 straight k end fraction end cell row cell 1 over k subscript p e n g g a n t i end subscript space end cell equals cell space fraction numerator 3 over denominator 2 straight k end fraction end cell row cell k subscript p e n g g a n t i end subscript space end cell equals cell space fraction numerator 2 straight k over denominator 3 end fraction end cell end table end style$

Kemudian dengan menggunakan persamaan Hukum Hooke, dapat dicari :

$begin mathsize 14px style table attributes columnalign right center left columnspacing 0px end attributes row cell F space end cell equals cell space k space times space increment x end cell row cell 1 comma 2 space end cell equals cell space fraction numerator 2 k over denominator 3 end fraction space left parenthesis 0 comma 006 right parenthesis end cell row cell 3 comma 6 space end cell equals cell space 0 comma 012 k end cell row cell k space end cell equals cell space fraction numerator 3 comma 6 over denominator 0 comma 012 end fraction end cell row cell k space end cell equals cell space 300 space Nm to the power of negative 1 end exponent end cell end table end style$

Sehingga besar konstanta masing-masing pegas adalah .

Jadi, jawaban yang tepat adalah C.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.7 (30 rating)

Rofianita

Pembahasan lengkap banget

Anon

Pembahasan lengkap banget Mudah dimengerti Makasih ❤️

Venti

Ini yang aku cari!

Erni Ngewi Leo

Pembahasan terpotong

Pertanyaan serupa

Perhatikan rangkaian pegas di bawah ini! Andaikan ada ujung bawah rangkaian pegas dipasang beban sedemikian rupa sehingga rangkaian itu secara keseluruhan bertambah panjang sejauh x . a. Hitu...

3.0

Jawaban terverifikasi

Dua susunan pegas ditunjukkan seperti pada gambar di bawah. Perbandingan pertambahan panjang susunan pegas (I) dan susunan pegas (II) adalah ....

5.0

Jawaban terverifikasi

Perhatikan gambar berikut. Jika susunan pegas di atas diberi beban bermassa 4 kg, pegas bertambah panjang 2 cm ( g = 10 m/s 2 ).Besar gaya yang diperlukan agar pertambahan panjang susunan pegas ...

4.3

Jawaban terverifikasi

Enam buah pegas identik disusun sehingga terbentuk seperti gambar di bawah. Pegas kemudian digantungi beban bermassa M . Jika konstanta masing-masing pegas100 N/m dan massabeban M sebesar5 kg, t...

5.0

Jawaban terverifikasi

Dua susunan pegas ditunjukkan seperti pada gambar di bawah. Perbandingan pertambahan panjang susunan pegas (I) dan susunan pegas (II) adalah ....

5.0

Jawaban terverifikasi