Iklan
Pertanyaan
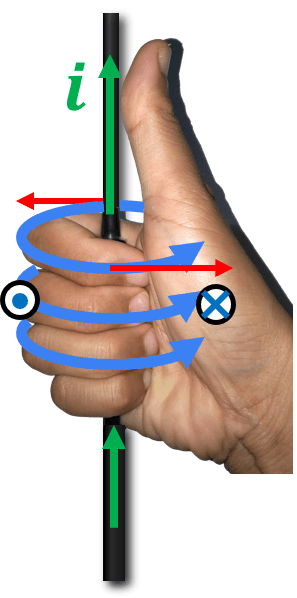
Titik P sebidang dengan kawat sejajar seperti gambar berikut. Jika B 1 dan B 2 merupakan induksi magnetik di titik P yang disebabkan oleh kawat berarus I 1 dan I 2 ,arah B 1 dan B 2 adalah ....
Titik P sebidang dengan kawat sejajar seperti gambar berikut.
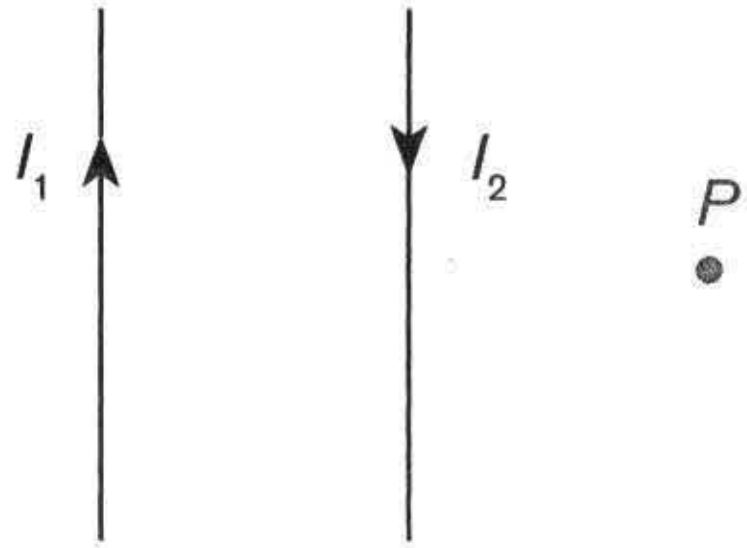
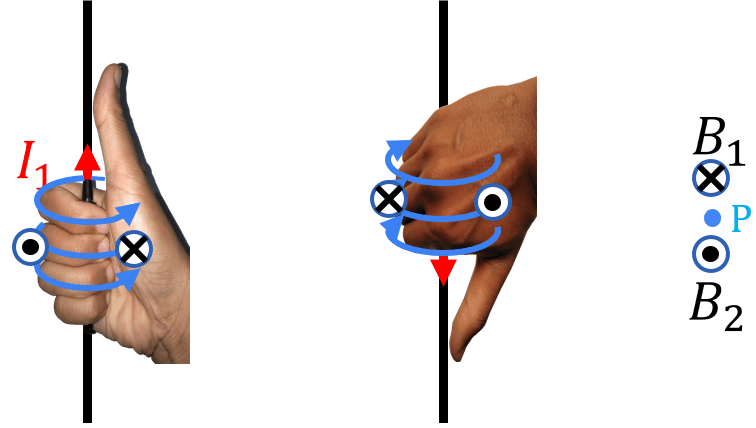
Jika B1 dan B2 merupakan induksi magnetik di titik P yang disebabkan oleh kawat berarus I1 dan I2, arah B1 dan B2 adalah ....
tegak lurus bidang kertas menuju pembaca
tegak lurus bidang kertas menjauhi pembaca
B1 menuju pembaca dan B2 menjauhi pembaca
B1 menjauhi pembaca dan B2 menuju pembaca
B1 ke kanan dan B2 ke kiri
Iklan
NP
N. Puspita
Master Teacher
Jawaban terverifikasi
70
5.0 (15 rating)
MR
Muhammad Rifqi Andika Hastoaji
Mudah dimengerti
d
dimasss
Makasih ❤️
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia