Tentukanlah sistem pertidaksamaan dari daerah yang diarsir pada gambar berikut!

Pembahasan

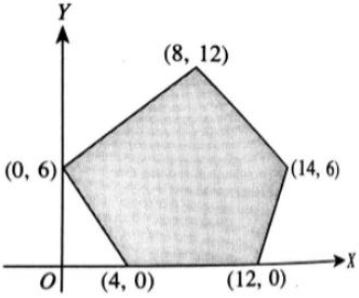
Perhatikan garis yang melalui titik ( 0 , 6 ) dan titik ( 4 , 0 ) , persamaan garis lurus yaitu : y 2 ​ − y 1 ​ y − y 1 ​ ​ 0 − 6 y − 6 ​ − 6 y − 6 ​ 4 ( y − 6 ) 4 y − 24 6 x + 4 y 3 x + 2 y ​ = = = = = = = ​ x 2 ​ − x 1 ​ x − x 1 ​ ​ 4 − 0 x − 0 ​ 4 x ​ − 6 x − 6 x 24 12 ​ Karenadaerah pertidaksamaannya ke atas maka pertidaksamaannya yaitu 3 x + 2 y ≥ 12 . Perhatikan garis yang melalui titik ( 0 , 6 ) dan titik ( 8 , 12 ) , persamaan garis lurus yaitu : y 2 ​ − y 1 ​ y − y 1 ​ ​ 12 − 6 y − 6 ​ 6 y − 6 ​ 8 ( y − 6 ) 8 y − 48 8 y − 6 x 4 y − 3 x ​ = = = = = = = ​ x 2 ​ − x 1 ​ x − x 1 ​ ​ 8 − 0 x − 0 ​ 8 x ​ 6 x 6 x 48 24 ​ Karenadaerah pertidaksamaannya ke bawah maka pertidaksamaannya yaitu 4 y − 3 x ≤ 24 . Perhatikan garis yang melalui titik ( 8 , 12 ) dan titik ( 14 , 6 ) , persamaan garis lurus yaitu : y 2 ​ − y 1 ​ y − y 1 ​ ​ 6 − 12 y − 12 ​ − 6 y − 12 ​ 6 ( y − 12 ) 6 y − 72 6 x + 6 y x + y ​ = = = = = = = ​ x 2 ​ − x 1 ​ x − x 1 ​ ​ 14 − 8 x − 8 ​ 6 x − 8 ​ − 6 ( x − 8 ) − 6 x + 48 120 20 ​ Karenadaerah pertidaksamaannya ke bawah maka pertidaksamaannya yaitu x + y ≤ 20 . Perhatikan garis yang melalui titik ( 14 , 6 ) dan titik ( 12 , 0 ) , persamaan garis lurus yaitu : y 2 ​ − y 1 ​ y − y 1 ​ ​ 0 − 6 y − 6 ​ − 6 y − 6 ​ − 2 ( y − 6 ) − 2 y + 12 6 x − 2 y 6 x − 2 y 3 x − y ​ = = = = = = = = ​ x 2 ​ − x 1 ​ x − x 1 ​ ​ 12 − 14 x − 14 ​ − 2 x − 14 ​ − 6 ( x − 14 ) − 6 x + 84 84 − 12 72 12 ​ Karenadaerah pertidaksamaannya ke atas maka pertidaksamaannya yaitu 3 x − y ≥ 12 . Karena daerah penyelesaian berada di atas sumbu x dan di sebelah kanan sumbu y maka x ≥ 0 dan y ≥ 0 . Dengan demikian,sistem pertidaksamaan dari daerah yang diarsir pada gambar tersebut adalah 3 x + 2 y ≥ 12 , 4 y − 3 x ≤ 24 , x + y ≤ 20 , 3 x − y ≥ 12 , x ≥ 0 dan y ≥ 0 .