Gambar pada diagram kartesius untuk mengetahui asimtot dan titik yang dilalui grafik fungsinya
Cari titik potong terhadap sumbu-X
y=x2+1x0=x2+1x0=x(x,y)=(0,0)
Titik (0,0) juga menandakan potong grafik terhadap sumbu-Y
Fungsi y=x2+1x tidak memiliki asimtot tegak karena x2+1=0
Asimtot datar
y===limx→∞f(x)limx→∞x2+1x0
Cari beberapa titik yang mewakili fungsi
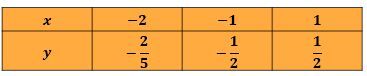
Sehingga grafiknya adalah
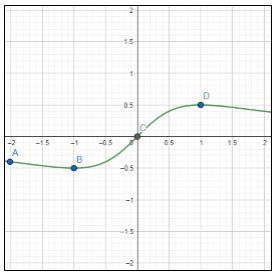
Dari penjabaran di atas diperoleh bahwa asimtot datar y=0 tidak hanya didekati tetapi juga dilewati oleh grafik, sehingga y=0 juga merupakan nilai dari fungsi. Serta dari gambar terihat bahwa grafik memiliki titik stasioner.
Ingat!
Turunan dari fungsi  adalah
adalah  .
.
Kita cari turunan dari fungsi  terlebih dahulu dengan menggunakan rumus:
terlebih dahulu dengan menggunakan rumus:

Diketahui fungsi  . Misal
. Misal  , maka
, maka  dan
dan  , maka
, maka  . Dengan demikian, turunan dari fungsi
. Dengan demikian, turunan dari fungsi  tersebut adalah
tersebut adalah

Selanjutnya akan dicari titik stasionernya

Penyebut tidak pernah bernilai nol, maka pembilang yang harus bernilai nol agar persamaan bernilai benar.

Untuk  , diperoleh
, diperoleh

Untuk  , diperoleh
, diperoleh

Maka nilai  berada di antara
berada di antara  hingga
hingga  .
.
Jadi, batasan nilai dari  untuk nilai
untuk nilai  yang real yaitu
yang real yaitu  .
.



















