Diketahui  . Dari pertidaksamaan tersebut, terbagi menjadi dua yaitu ketika
. Dari pertidaksamaan tersebut, terbagi menjadi dua yaitu ketika  dan
dan  .
.
a. 
Ketika  diperoleh:
diperoleh:

 dan
dan 

Lalu, ketika  , jika
, jika  maka:
maka:



Penyelesaian dari pertidaksamaan di atas sebagai berikut.

Nilai  yang memenuhi saat sama dengan
yang memenuhi saat sama dengan  sebagai berikut.
sebagai berikut.

Lalu, nilai  di atas dapat dituliskan pada garis bilangan sebagai berikut.
di atas dapat dituliskan pada garis bilangan sebagai berikut.
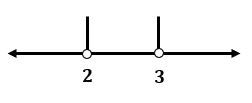
Berdasarkan garis bilangan di atas, terdapat  daerah yaitu
daerah yaitu  ,
,  , dan
, dan  . Uji titik pada setiap daerah tersebut sebagai berikut.
. Uji titik pada setiap daerah tersebut sebagai berikut.
Ketika  , pilih
, pilih  maka diperoleh:
maka diperoleh:


Berdasarkan uji titik di atas, ketika  , nilai
, nilai  negatif atau kurang dari
negatif atau kurang dari  .
.
Ketika  , pilih
, pilih  , maka diperoleh:
, maka diperoleh:


Berdasarkan uji titik di atas, ketika  , nilai
, nilai  positif atau lebih dari
positif atau lebih dari  .
.
Ketika  , pilih
, pilih  , maka diperoleh:
, maka diperoleh:


Berdasarkan uji titik di atas, ketika  , nilai
, nilai  negatif atau kurang dari
negatif atau kurang dari  .
.
Hasil di atas dapat dituliskan pada garis bilangan sebagai berikut.
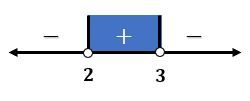
Berdasarkan garis bilangan di atas, nilai  yang memenuhi pertidaksamaan
yang memenuhi pertidaksamaan  adalah
adalah  .
.


Nilai  yang memenuhi saat sama dengan
yang memenuhi saat sama dengan  sebagai berikut.
sebagai berikut.

Lalu, nilai  di atas dapat dituliskan pada garis bilangan sebagai berikut.
di atas dapat dituliskan pada garis bilangan sebagai berikut.

Berdasarkan garis bilangan di atas, terdapat  daerah yaitu
daerah yaitu  dan
dan  . Uji titik pada setiap daerah tersebut sebagai berikut.
. Uji titik pada setiap daerah tersebut sebagai berikut.
Ketika  , pilih
, pilih  maka diperoleh:
maka diperoleh:


Berdasarkan uji titik di atas, ketika  , nilai
, nilai  positif atau lebih dari
positif atau lebih dari  .
.
Ketika  , pilih
, pilih  , maka diperoleh:
, maka diperoleh:


Berdasarkan uji titik di atas, ketika  , nilai
, nilai  positif atau lebih dari
positif atau lebih dari  .
.
Hasil di atas dapat dituliskan pada garis bilangan sebagai berikut.
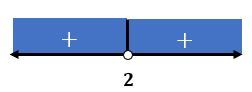
Berdasarkan garis bilangan di atas, nilai  yang memenuhi pertidaksamaan
yang memenuhi pertidaksamaan  adalah
adalah  atau
atau  .
.
Kemudian, penyelesaian dari pertidaksamaan  ketika
ketika  adalah irisan dari penyelesaian
adalah irisan dari penyelesaian  ,
,  ,
,  , dan
, dan  . Irisan tersebut dapat ditentukan dengan menggunakan garis bilangan sebagai berikut.
. Irisan tersebut dapat ditentukan dengan menggunakan garis bilangan sebagai berikut.
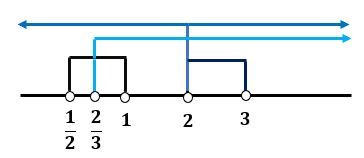
Berdasarkan garis bilangan di atas, ketika  , tidak ada nilai
, tidak ada nilai  yang memenuhi pertidaksamaan
yang memenuhi pertidaksamaan  .
.
b. 
Ketika  diperoleh:
diperoleh:

Lalu, ketika  , jika
, jika  maka:
maka:



Penyelesaian dari pertidaksamaan di atas sebagai berikut.

Berdasarkan uraian sebelumnya, garis bilangan yang berkaitan dengan pertidaksamaan di atas sebagai berikut.
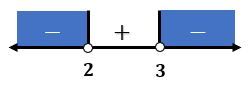
Berdasarkan garis bilangan di atas, penyelesaian dari  adalah
adalah  atau
atau  .
.
Berdasarkan uraian sebelumnya, penyelesaian dari  adalah
adalah  .
.
Berdasarkan uraian sebelumnya, penyelesaian dari  adalah
adalah  atau
atau  .
.
Selanjutnya, penyelesaian dari pertidaksamaan  ketika
ketika  adalah irisan dari penyelesaian
adalah irisan dari penyelesaian  ,
,  ,
,  , dan
, dan  . Irisan tersebut dapat ditentukan dengan menggunakan garis bilangan sebagai berikut.
. Irisan tersebut dapat ditentukan dengan menggunakan garis bilangan sebagai berikut.
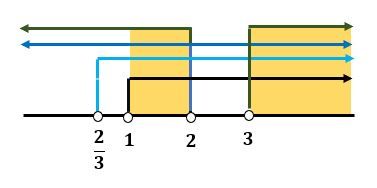
Berdasarkan garis bilangan di atas, ketika  ,
, yang memenuhi
yang memenuhi  adalah
adalah  atau
atau  .
.
Kemudian, penyelesaian dari pertidaksamaan  adalah gabungan dari penyelesaian ketika
adalah gabungan dari penyelesaian ketika  dan
dan  . Gabungan dari kedua penyelesaian tersebut adalah
. Gabungan dari kedua penyelesaian tersebut adalah  atau
atau  .
.
Dengan demikian, penyelesaian pertidaksamaan  adalah
adalah  atau
atau  .
.





















