Tentukan median dan kuartil dari data yang dinyatakan dalam daftar distribusi frekuensi berikut. c.

Pembahasan

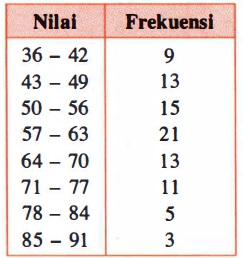
Ingat kembali rumus kuartil bawah ( Q 1 ​ ) , median ( Q 2 ​ ) , dan kuartil atas ( Q 3 ​ ) pada data berkelompok sebagai berikut: Q 1 ​ = L 1 ​ + c ⎝ ⎛ ​ f 1 ​ 4 1 ​ n − F 1 ​ ​ ⎠ ⎞ ​ Q 2 ​ = L 2 ​ + c ⎝ ⎛ ​ f 2 ​ 2 1 ​ n − F 2 ​ ​ ⎠ ⎞ ​ Q 3 ​ = L 3 ​ + c ⎝ ⎛ ​ f 3 ​ 4 3 ​ n − F 3 ​ ​ ⎠ ⎞ ​ dimana L 1 , 2 , 3 ​ = tepi bawah kelas kuartil bawah, median, kuartil atas n = ukuran data (jumlah frekuensi) f 1 , 2 , 3 ​ = frekuensi pada interval kelas kuartil bawah, median dan kuartil atas F 1 , 2 , 3 ​ = frekuensi kumulatif sebelum kelas kuartil bawah, median dan kuartil atas c = panjang kelas Oleh karena itu, berdasarkan tabel distribusi frekuensi di atas, kita menambahkan satu kolom yaitu frekuensi kumulatif seperti pada tabel di bawah ini 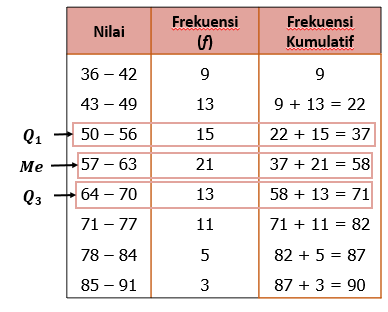Interval kelas kuartil bawahterletak pada 50 − 56 diperoleh dari 4 1 ​ n = 4 1 ​ × 90 = 22 , 5 (lihat dari frekuensi kumulatif), dengan n = 90 , L 1 ​ = 50 − 0 , 5 = 49 , 5 , f 1 ​ = 15 , F 1 ​ = 22 , c = 7 Q 1 ​ ​ = = = = = ​ L 1 ​ + c ⎝ ⎛ ​ f 1 ​ 4 1 ​ n − F 1 ​ ​ ⎠ ⎞ ​ 49 , 5 + 7 ⋅ ⎝ ⎛ ​ 15 4 1 ​ ⋅ 90 − 22 ​ ⎠ ⎞ ​ 49 , 5 + 7 ⋅ ( 15 22 , 5 − 22 ​ ) 49 , 5 + 0 , 23 49 , 73 ​ Interval kelas medianterletak pada 57 − 63 diperoleh dari 2 1 ​ n = 2 1 ​ × 90 = 45 (lihat dari frekuensi kumulatif), dengan n = 90 , L 2 ​ = 57 − 0 , 5 = 56 , 5 , f 2 ​ = 21 , F 2 ​ = 37 , c = 7 Q 2 ​ ​ = = = = = ​ L 2 ​ + c ⎝ ⎛ ​ f 2 ​ 2 1 ​ n − F 2 ​ ​ ⎠ ⎞ ​ 56 , 5 + 7 ⋅ ⎝ ⎛ ​ 21 2 1 ​ ⋅ 90 − 37 ​ ⎠ ⎞ ​ 56 , 5 + 7 ⋅ ( 21 45 − 37 ​ ) 56 , 5 + 2 , 67 59 , 17 ​ Interval kelas kuartil atas terletak pada 64 − 70 diperoleh dari 4 3 ​ n = 4 3 ​ × 90 = 67 , 5 (lihat dari frekuensi kumulatif), dengan n = 90 , L 3 ​ = 64 − 0 , 5 = 63 , 5 , f 3 ​ = 13 , F 3 ​ = 58 , c = 7 Q 3 ​ ​ = = = = = ​ L 3 ​ + c ⎝ ⎛ ​ f 3 ​ 4 3 ​ n − F 3 ​ ​ ⎠ ⎞ ​ 63 , 5 + 7 ⋅ ⎝ ⎛ ​ 13 4 3 ​ ⋅ 90 − 58 ​ ⎠ ⎞ ​ 63 , 5 + 7 ⋅ ( 13 67 , 5 − 58 ​ ) 63 , 5 + 5 , 12 68 , 62 ​ Dengan demikian, kuartil bawah Q 1 ​ = 49 , 73 , median Q 2 ​ = 59 , 17 , dan kuartil atas Q 3 ​ = 68 , 62 .