Pertanyaan

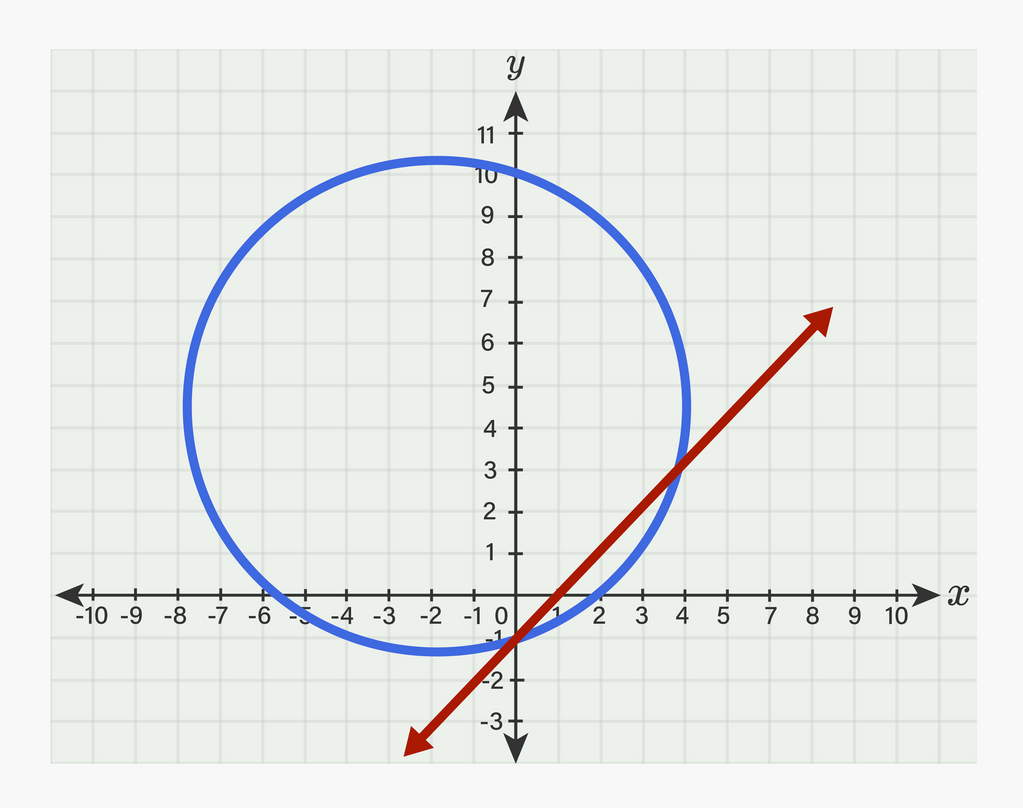
Tentukan koordinat titik potong antara garis dan lingkaran berikut ini dan lukislah dalam koordinat Cartesius. a. x 2 + y 2 + 4 x − 9 y − 10 = 0 dan x − y − 1 = 0

Tentukan koordinat titik potong antara garis dan lingkaran berikut ini dan lukislah dalam koordinat Cartesius.

a. $x^{2} + y^{2} + 4 x - 9 y - 10 = 0$ dan $x - y - 1 = 0$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

A. Salim

Master Teacher

Mahasiswa/Alumni Universitas Pelita Harapan

Jawaban terverifikasi

Jawaban

garis dan lingkaran tersebut berpotongan di titik ( 0 , − 1 ) dan ( 2 7 , 2 5 ) .

garis dan lingkaran tersebut berpotongan di titik

(0, - 1)

dan

(\frac{7}{2}, \frac{5}{2})

Pembahasan

Misalkan diketahui persamaan garis lurus g dan persamaanlingkaran L . Titik potong garis g dengan lingkaran L dapat ditentukandengan langkah-langkah berikut. 1. Substitusikan persamaan garis g ke dalam persamaan lingkaran L sehingga diperoleh sebuah persamaan kuadrat. 2. Faktorkan persamaan kuadrat dari hasil langkah 1 untuk memperoleh nilai x . 3. Untuk menentukan nilai y , substitusikan nilai x yang diperoleh dari langkah 2 ke dalam persamaangaris g atau persamaan lingkaran L . Penyelesaian soal di atas adalah sebagai berikut. Substitusikanpersamaan garis x − y − 1 = 0 ke dalam persamaanlingkaran x 2 + y 2 + 4 x − 9 y − 10 = 0 sehingga diperoleh hasilsebagai berikut. x − y − 1 = 0 ↔ y = x − 1 x 2 + y 2 + 4 x − 9 y − 10 x 2 + ( x − 1 ) 2 + 4 x − 9 ( x − 1 ) − 10 x 2 + x 2 − 2 x + 1 + 4 x − 9 x + 9 − 10 2 x 2 − 7 x x ( 2 x − 7 ) = = = = = 0 0 0 0 0 x = 0 atau x = 2 7 Untuk nilai x = 0 dapat ditentukan nilai y sebagai berikut. y = = = x − 1 0 − 1 − 1 Diperoleh titik potong ( 0 , − 1 ) . Untuk nilai x = 2 7 dapat ditentukan nilai y sebagai berikut. y = = = x − 1 2 7 − 1 2 5 Diperoleh titik potong ( 2 7 , 2 5 ) Garis dan lingkaran tersebut dapat digambarkan sebagai berikut. Menentukan pusat dan jari-jari lingkaran x 2 + y 2 + 4 x − 9 y − 10 = 0 . Pusat ( − 2 A , − 2 B ) = ( − 2 4 , − 2 − 9 ) = ( − 2 , 2 9 ) Jari-jari lingkaran: r = = = = = = ( − 2 A ) 2 + ( − 2 B ) 2 − C ( − 2 4 ) 2 + ( − 2 − 9 ) 2 + 10 4 + 4 81 + 10 4 16 + 81 + 40 34 , 25 5 , 85 Untuk menggambar garis, tentukan titik potong garis dengan sumbu x dan sumbu y diperoleh titik potong ( 1 , 0 ) dan ( 0 , − 1 ) Dengan demikian, garis dan lingkaran tersebut berpotongan di titik ( 0 , − 1 ) dan ( 2 7 , 2 5 ) .

Misalkan diketahui persamaan garis lurus $g$ dan persamaan lingkaran $L$ . Titik potong garis $g$ dengan lingkaran $L$ dapat ditentukan dengan langkah-langkah berikut.

1. Substitusikan persamaan garis $g$ ke dalam persamaan lingkaran $L$ sehingga diperoleh sebuah persamaan kuadrat.

2. Faktorkan persamaan kuadrat dari hasil langkah 1 untuk memperoleh nilai $x$ .

3. Untuk menentukan nilai $y$ , substitusikan nilai $x$ yang diperoleh dari langkah 2 ke dalam persamaan garis $g$ atau persamaan lingkaran $L$ .

Penyelesaian soal di atas adalah sebagai berikut.

Substitusikan persamaan garis $x - y - 1 = 0$ ke dalam persamaan lingkaran $x^{2} + y^{2} + 4 x - 9 y - 10 = 0$ sehingga diperoleh hasil sebagai berikut.

$x - y - 1 = 0 \leftrightarrow y = x - 1$

$x^{2} + y^{2} + 4 x - 9 y - 10 x^{2} + (x - 1)^{2} + 4 x - 9 (x - 1) - 10 x^{2} + x^{2} - 2 x + 1 + 4 x - 9 x + 9 - 10 2 x^{2} - 7 x x (2 x - 7) = = = = = 00000$

$x = 0 atau x = \frac{7}{2}$

Untuk nilai $x = 0$ dapat ditentukan nilai $y$ sebagai berikut.

$y = = = x - 1 0 - 1 - 1$

Diperoleh titik potong $(0, - 1)$ .

Untuk nilai $x = \frac{7}{2}$ dapat ditentukan nilai $y$ sebagai berikut.

$y = = = x - 1 \frac{7}{2} - 1 \frac{5}{2}$

Diperoleh titik potong $(\frac{7}{2}, \frac{5}{2})$

Garis dan lingkaran tersebut dapat digambarkan sebagai berikut.

Menentukan pusat dan jari-jari lingkaran $x^{2} + y^{2} + 4 x - 9 y - 10 = 0$ .

Pusat $(\frac{A}{- 2}, \frac{B}{- 2}) = (\frac{4}{- 2}, \frac{- 9}{- 2}) = (- 2, \frac{9}{2})$

Jari-jari lingkaran:

$r = = = = = = (\frac{A}{- 2})^{2} + (\frac{B}{- 2})^{2} - C (\frac{4}{- 2})^{2} + (\frac{- 9}{- 2})^{2} + 10 4 + \frac{81}{4} + 10 \frac{16 + 81 + 40}{4} 34, 25 5, 85$

Untuk menggambar garis, tentukan titik potong garis dengan sumbu $x$ dan sumbu $y$ diperoleh titik potong $(1, 0)$ dan $(0, - 1)$

Dengan demikian, garis dan lingkaran tersebut berpotongan di titik $(0, - 1)$ dan $(\frac{7}{2}, \frac{5}{2})$ .

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.5 (7 rating)

Asra Ozali

Ini yang aku cari!

Aulia Donna Agnesia Harahap

Makasih ❤️

Pertanyaan serupa

Tentukan koordinat titik potong antara garis dan lingkaran berikut ini dan lukislah dalam koordinat Cartesius. b. x − 2 y + 1 = 0 dan x 2 + y 2 − 2 x − 4 y + 4 = 0

4.2

Jawaban terverifikasi

Tentukan koordinat titik potong antara garis dan lingkaran berikut ini dan lukislah dalam koordinat Cartesius. b. x − 2 y + 1 = 0 dan x 2 + y 2 − 2 x − 4 y + 4 = 0

4.2

Jawaban terverifikasi

Tentukan koordinat titik potong lingkaran L ≡ x 2 + y 2 − 6 x − 8 y = 0 dengan sumbu X positif dan sumbu Y positif.

3.7

Jawaban terverifikasi

Garis x = 2 y + 4 memotong lingkaran x 2 + y 2 − 6 y − 16 = 0 . Panjang segmen dari garis yang terletak di dalam lingkaran itu adalah ...

4.6

Jawaban terverifikasi

Garis x = 2 y + 4 memotong lingkaran x 2 + y 2 − 6 y − 16 = 0 . Panjang segmen dari garis yang terletak di dalam lingkaran itu adalah ...

4.6

Jawaban terverifikasi