Tentukan hamparan dan simpangan kuartil dari data berikut!

Pembahasan

Ingat bahwa: Hamparan dapat dinyatakan melalui rumus berikut. Hamparan = Q 3 ​ − Q 1 ​ dengan Q 3 ​ = kuartil tiga ( kuartil atas ) Q 1 ​ = kuartil satu ( kuartil bawah ) Ingat pula bahwa rumus kuartil adalah Q i ​ = L Q i ​ ​ + f Q i ​ ​ 4 i ​ n − f k ​ ​ × p dengan Q i ​ L Q i ​ ​ i n f k ​ f Q i ​ ​ p ​ = = = = = = = ​ kuartil ke − i tepi bawah kelas kuartil 1 , 2 , 3 banyak data frekuensi kumulatif sebelum kelas kuartil frekuensi kelas kuartil panjang kelas ​ 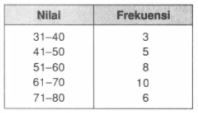Berdasarkan data di atas diperoleh banyak datanya adalah n = 3 + 5 + 8 + 10 + 6 = 32 . Kuartil 1: Q 1 ​ ​ = = = ​ data ke − 4 1 ​ n data ke − 4 1 ​ × 32 data ke − 8 ​ Sehingga diperoleh Q 1 ​ data ke- 8 pada interval 41 − 50 . L Q 1 ​ ​ = 41 − 0 , 5 = 40 , 5 f k ​ = 3 f Q 1 ​ ​ = 5 p = 41 − 31 = 10 Q 1 ​ ​ = = = = = = ​ L Q i ​ ​ + f Q 1 ​ ​ 4 1 ​ n − f k ​ ​ × p 40 , 5 + 5 8 − 3 ​ × 10 40 , 5 + 5 5 ​ × 10 40 , 5 + 5 50 ​ 40 , 5 + 10 50 , 5 ​ Kuartil 3: Q 3 ​ ​ = = = ​ data ke − 4 3 ​ n data ke − 4 3 ​ × 32 data ke − 24 ​ Sehingga diperoleh Q 3 ​ data ke- 24 pada interval 61 − 70 . L Q 3 ​ ​ = 61 − 0 , 5 = 60 , 5 f k ​ = 3 + 5 + 8 = 16 f Q 3 ​ ​ = 10 p = 10 Q 3 ​ ​ = = = = = = ​ L Q 3 ​ ​ + f Q 3 ​ ​ 4 3 ​ n − f k ​ ​ × p 60 , 5 + 10 24 − 16 ​ × 10 60 , 5 + 10 8 ​ × 10 60 , 5 + 10 80 ​ 60 , 5 + 8 68 , 5 ​ Oleh karena itu diperoleh hamparannya adalah hamparan ​ = = = ​ Q 3 ​ − Q 1 ​ 68 , 5 − 50 , 5 18 ​ Ingat bahwa: Simpangan kuartil dapat dinyatakan melalui rumus berikut. simpangan kuartil = 2 1 ​ × hamparan Pada soal sebelumnya, diperoleh nilai hamparannya adalah 18 , sehingga simpangan kuartilnya adalah simpangan kuartil ​ = = = ​ 2 1 ​ × hamparan 2 1 ​ × 18 9 ​ Dengan demikian, hamparan data di atas adalah 18 dan simpangan kuartilnya adalah 9 .