Diketahui data sebagai berikut. 50 39 38 44 ​ 47 37 39 45 ​ 44 40 42 42 ​ 41 43 45 43 ​ 38 49 48 46 ​ 36 50 51 44 ​ 50 52 49 41 ​ 48 47 46 45 ​ 45 44 43 46 ​ 42 41 41 44 ​ 1. Buatlah daftar distribusi frekuensi berkelompok untuk data di atas! 2. Tentukan hamparannya! 3. Tentukan simpangan kuartilnya!

Pembahasan

1.Untuk menentukan banyaknya kelas, akan ditentukan dengan aturan Sturgess, yaitu k = 1 + 3 , 3 lo g n Ukuran data: n = 40 Data terkecil = 36 dan data terbesar = 52 Jangkauan = 52 − 36 = 16 Sehingga diperoleh banyak kelasnya adalah k ​ = = = = = ​ 1 + 3 , 3 lo g n 1 + 3 , 3 lo g 40 1 + 3 , 3 ( 1 , 602 ) 1 + 5 , 2866 6 , 2866 ​ Nilai k dibulatkan menjadi 6 . panjang kelas ​ = = = ​ banyak kelas jangkauan ​ 6 16 ​ 2 , 67 ​ Panjang kelas dapat dibulatkan menjadi 3 . Jadi, kelas pertama adalah 36 − 38 , kelas kedua 39 − 41 , dan seterusnya. 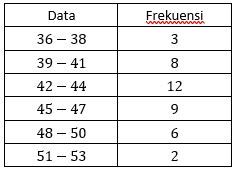Dengan demikian, diperoleh tabel distribusi frekuensinya adalah 2. Ingat bahwa: Hamparan dapat dinyatakan melalui rumus berikut. Hamparan = Q 3 ​ − Q 1 ​ dengan Q 3 ​ = kuartil tiga ( kuartil atas ) Q 1 ​ = kuartil satu ( kuartil bawah ) Ingat pula bahwa rumus kuartil adalah Q i ​ = L Q i ​ ​ + f Q i ​ ​ 4 i ​ n − f k ​ ​ × p dengan Q i ​ L Q i ​ ​ i n f k ​ f Q i ​ ​ p ​ = = = = = = = ​ kuartil ke − i tepi bawah kelas kuartil 1 , 2 , 3 banyak data frekuensi kumulatif sebelum kelas kuartil frekuensi kelas kuartil panjang kelas ​ Kuartil 1: Q 1 ​ ​ = = = ​ data ke − 4 1 ​ n data ke − 4 1 ​ × 40 data ke − 10 ​ Sehingga diperoleh Q 1 ​ data ke- 10 pada interval 39 − 41 . L Q 1 ​ ​ = 39 − 0 , 5 = 38 , 5 f k ​ = 3 f Q 1 ​ ​ = 8 p = 3 Q 1 ​ ​ = = = = = = ​ L Q i ​ ​ + f Q 1 ​ ​ 4 1 ​ n − f k ​ ​ × p 38 , 5 + 8 10 − 3 ​ × 3 38 , 5 + 8 7 ​ × 3 38 , 5 + 8 21 ​ 38 , 5 + 2 , 625 41 , 125 ​ Kuartil 3: Q 3 ​ ​ = = = ​ data ke − 4 3 ​ n data ke − 4 3 ​ × 40 data ke − 30 ​ Sehingga diperoleh Q 3 ​ data ke- 30 pada interval 45 − 47 . L Q 1 ​ ​ = 45 − 0 , 5 = 44 , 5 f k ​ = 3 + 8 + 12 = 23 f Q 1 ​ ​ = 9 p = 3 Q 3 ​ ​ = = = = = = ​ L Q 3 ​ ​ + f Q 3 ​ ​ 4 3 ​ n − f k ​ ​ × p 44 , 5 + 9 30 − 23 ​ × 3 44 , 5 + 9 7 ​ × 3 44 , 5 + 9 21 ​ 44 , 5 + 2 , 34 46 , 84 ​ Oleh karena itu, nilai hamparannya adalah hamparan ​ = = = ​ Q 3 ​ − Q 1 ​ 46 , 84 − 41 , 125 5 , 715 ​ Dengan demikian, hamparan dari data di atas adalah 5 , 715 . 3. Ingat bahwa: Simpangan kuartil dapat dinyatakan melalui rumus berikut. simpangan kuartil = 2 1 ​ × hamparan Pada soal sebelumnya, diperoleh nilai hamparannya adalah 5 , 715 , sehingga simpangan kuartilnya adalah simpangan kuartil ​ = = = ​ 2 1 ​ × hamparan 2 1 ​ × 5 , 715 2 , 8575 ​ Dengan demikian, simpangan kuartil data di atas adalah 2 , 8575 .