Jawaban yang benar untuk pertanyaan tersebut adalah A.
Persamaan hiperbola yang berpusat di (p, q) dan fokus terletak pada sumbu x adalah sebagai berikut.
a2(x−p)2−b2(y−q)2=1
Persamaan hiperbola yang berpusat di (p, q) dan fokus terletak pada sumbu y adalah sebagai berikut.
a2(y−q)2−b2(x−p)2=1
Gradien persamaan garis asimtot hiperbola yang berpusat di (p, q) dan fokus terletak pada sumbu x adalah m=±ab
Gradien persamaan garis asimtot hiperbola yang berpusat di (p, q) dan fokus terletak pada sumbu y adalah m=±ba
Diketahui hiperbola mempunyai dua asimtot yang saling tegak lurus. Titik potong kedua asimtot tersebut dengan sumbu y adalah (0, 1) dan (0, 3).
Kedua asimtot hiperbola tersebut saling tegak lurus sehingga (a=b). Diperoleh persamaan hiperbola sebagai berikut.
(x−p)2−(y−q)2=a2
atau
−(x−p)2+(y−q)2=a2
Titik potong kedua asimtot dengan sumbu y adalah (0, 1) dan (0, 3). Gradien kedua asimtot yang saling tegak lurus berlaku m1⋅m2=−1
Persamaan asimtot yang melalui titik (0, 1) dan gradien m=1, yaitu
y−y1y−1y−1y====m(x−x1)1(x−0)xx+1
Persamaan asimtot yang melalui titik (0, 3) dan gradien m=−1, yaitu
y−y1y−3y−3y====m(x−x1)−1(x−0)−x−x+3
Titik pusat hiperbola dicari dengan y1=y2
x+12xx===−x+321
Diperoleh y=x+1=1+1=2
Titik pusat hiperbola, yaitu (1, 2)
Hiperbola tersebut dapat digambarkan sebagai berikut.
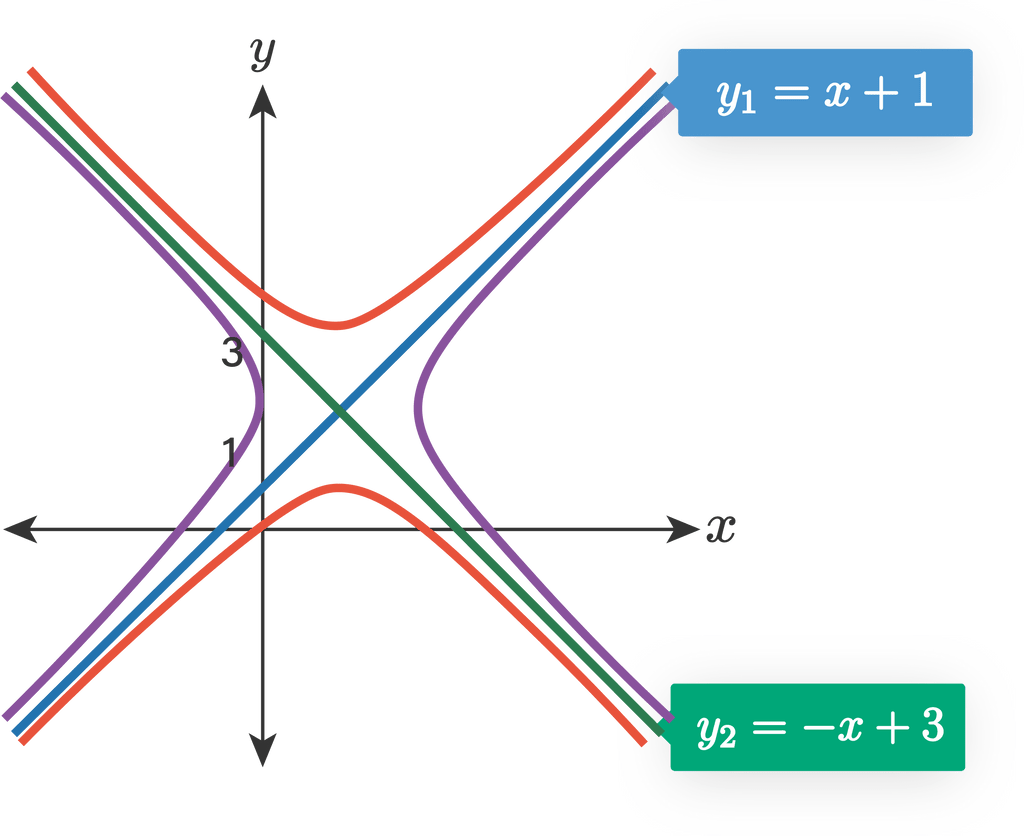
Dari gambar tersebut didapatkan a=b=1 sehingga persamaan parabola yang mungkin adalah sebagai berikut.
Hiperbola horizontal:
(x−p)2−(y−q)2(x−1)−(y−2)==a21
Atau hiperbola vertikal:
−(x−p)2+(y−q)2−(x−1)2+(y−2)2==a21
Oleh karena itu, jawaban yang benar adalah A.
















