Pertanyaan

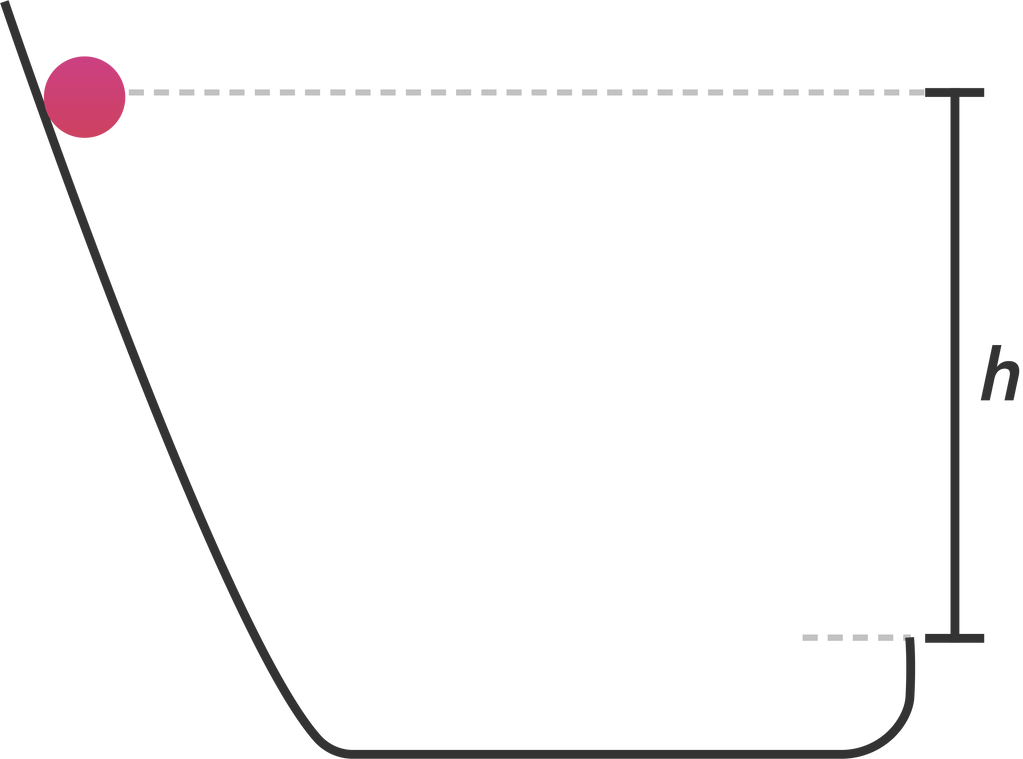
Sebuah bola bermassa M dan jari-jari R memiliki momen inersia I = 5 2 M R 2 . Bola dibebaskan dari keadaan diam danmenggelinding menuruni bidang miring tanpa kehilangan energikarena gesekan. Bola terlempar vertikal ke atas, keluar dari bidang miring seperti ditunjukkan dalam diagram mencapai ketinggian maksimum y maks di atas titik tempat bola meninggalkan bidang. Ketinggian maksimum bola y maks (dinyatakan dalam h ) besarnya adalah...

Sebuah bola bermassa M dan jari-jari R memiliki momen inersia $I = \frac{2}{5} M R^{2}$ . Bola dibebaskan dari keadaan diam dan menggelinding menuruni bidang miring tanpa kehilangan energi karena gesekan. Bola terlempar vertikal ke atas, keluar dari bidang miring seperti ditunjukkan dalam diagram mencapai ketinggian maksimum y_maks di atas titik tempat bola meninggalkan bidang. Ketinggian maksimum bola y_maks (dinyatakan dalam h) besarnya adalah...

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

A. Aulia

Master Teacher

Jawaban terverifikasi

Jawaban

jawaban yang tepat adalah C.

Pembahasan

Diketahui Massa = m Jaari-jari = R Bola menggelinding dan terlempar ke atas Ditanyakan Ketinggian maksimum bola y maks (dinyatakan dalam h ) Jawab Sebelum mencari ketinggian maksimum bola, kita harus menghitung kecepatan bola saat meninggalkan bidang menggunakan persamaan dari hukum kekekalan energi mekanik. Karena momen inersia bola dan kecepatan sudut , maka persamaan tersebut menjadi: Jadi, saat bola meninggalkan bidang miring, kecepatannya adalah . Saat bola mencapai ketinggian maksimum, maka kecepatan bola adalah nol ( v = 0). Dengan menggunakan persamaan GLBB, maka ketinggian maksimum bola dapat dihitung yaitu sebagai berikut. Dengan demikian, ketinggian maksimum bola y maks adalah . Jadi, jawaban yang tepat adalah C.

Diketahui
Massa = m
Jaari-jari = R
I equals 2 over 5 M R squared
Bola menggelinding dan terlempar ke atas

Ditanyakan
Ketinggian maksimum bola y_maks (dinyatakan dalam h)

Jawab
Sebelum mencari ketinggian maksimum bola, kita harus menghitung kecepatan bola saat meninggalkan bidang menggunakan persamaan dari hukum kekekalan energi mekanik.

table attributes columnalign right center left columnspacing 0px end attributes row cell E P subscript 1 plus E K subscript 1 end cell equals cell E P subscript 2 plus E K subscript 2 end cell row cell M g h plus 0 end cell equals cell 1 half M v squared plus 1 half I omega squared end cell end table

Karena momen inersia bola I equals 2 over 5 M R squared dan kecepatan sudut omega equals v over R , maka persamaan tersebut menjadi:

$table attributes columnalign right center left columnspacing 0px end attributes row cell E P subscript 1 plus E K subscript 1 end cell equals cell E P subscript 2 plus E K subscript 2 end cell row cell M g h plus 0 end cell equals cell 1 half M v squared plus 1 half I omega squared end cell row cell M g h end cell equals cell 1 half M v squared plus 1 half open parentheses 2 over 5 M R squared close parentheses open parentheses v over R close parentheses squared end cell row cell M g h end cell equals cell 1 half M v squared plus 1 fifth M v squared end cell row cell M g h end cell equals cell 7 over 10 M v squared end cell row cell up diagonal strike M g h end cell equals cell 7 over 10 up diagonal strike M v squared end cell row cell g h end cell equals cell 7 over 10 v squared end cell row v equals cell square root of fraction numerator 10 g h over denominator 7 end fraction end root end cell end table$

Jadi, saat bola meninggalkan bidang miring, kecepatannya adalah $table attributes columnalign right center left columnspacing 0px end attributes row v equals cell square root of fraction numerator 10 g h over denominator 7 end fraction end root end cell end table$ .

Saat bola mencapai ketinggian maksimum, maka kecepatan bola adalah nol (v = 0). Dengan menggunakan persamaan GLBB, maka ketinggian maksimum bola dapat dihitung yaitu sebagai berikut.

$y subscript m a k s end subscript equals fraction numerator v subscript o squared over denominator 2 g end fraction y subscript m a k s end subscript equals fraction numerator begin display style bevelled fraction numerator 10 g h over denominator 7 end fraction end style over denominator 2 g end fraction y subscript m a k s end subscript equals fraction numerator 5 h over denominator 7 end fraction$

Dengan demikian, ketinggian maksimum bola y_maks adalah .

Jadi, jawaban yang tepat adalah C.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.8 (6 rating)

Dini Wulandari

Bantu banget

SITI ZAHARA

Makasih ❤️

Pertanyaan serupa

Dua buah bola pejal yang identik berada pada puncak dua bidang miring yang berbeda. Bola pejal pertama berada pada bidang miring yang permukaannya kasar sedangkan bola pejal kedua berada pada bidang m...

5.0

Jawaban terverifikasi

Tentukan besamya energi kinetik total dari sebuah silinder beronggayang sedang menggelinding pada sebuah bidang miring dengan kelajuankonstanta 4 m/sjika diketahui massanya 20 kg, jari-jari lingkarand...

4.6

Jawaban terverifikasi

5.0

Jawaban terverifikasi

4.6

Jawaban terverifikasi

Sebuah silinder dengan massa m dan jari-jari r berada di atas bidang miring, kemudian silinder menggelinding. Jika momen inersia silinder I = 2 1 m r 2 , tentukan perbandingan kecepatan saat silinde...

3.7

Jawaban terverifikasi