Pertanyaan

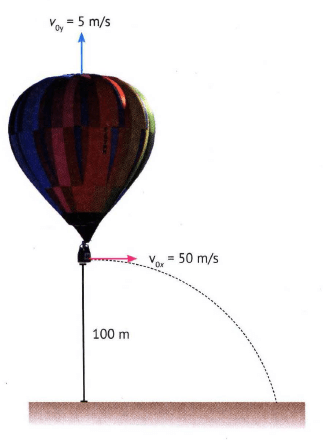
Sebuah balon udara sedang berada di ketinggian 100 m di atas tanah. Balon udara tersebut bergerak vertikal ke atas dengan kecepatan 5 m/s, pada saat itu ditembakkan sebuah peluru arah mendatar dengan kecepatan 50 m/s. Tentukan kapan, dimana kecepatan peluru saat mencapai titik tertinggi dan mencapai tanah!

Sebuah balon udara sedang berada di ketinggian 100 m di atas tanah. Balon udara tersebut bergerak vertikal ke atas dengan kecepatan 5 m/s, pada saat itu ditembakkan sebuah peluru arah mendatar dengan kecepatan 50 m/s. Tentukan kapan, dimana kecepatan peluru saat mencapai titik tertinggi dan mencapai tanah! $\;\;$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

N. Puspita

Master Teacher

Jawaban terverifikasi

Jawaban

peluru mencapai titik tertinggi setelah bergerak selama 0,5 s dan pada koordinat ( 25 ; 101 , 25 ) m , sedangkan mencapai tanah setelah bergerak 5 s.

peluru mencapai titik tertinggi setelah bergerak selama 0,5 s dan pada koordinat

(25; 101, 25) m

, sedangkan mencapai tanah setelah bergerak 5 s.

Pembahasan

Diketahui: v 0 x = 50 m / s v 0 y = 5 m / s y 0 = 100 m g = 10 m / s 2 Ditanya: t hma x , koordinat h ma x , dan t x ma x ? Pembahasan: Saat mencapai titik tertinggi v y = 0 v y 10 t t hma x = = = = v 0 y − g t 5 − 10 t 5 0 , 5 s Posisi saat mencapai titik tertinggi y = = = = y 0 + v 0 y t − 2 1 g t 2 100 + 5 ( 0 , 5 ) − 2 1 10 ( 0 , 5 ) 2 100 + 2 , 5 − 1 , 25 101 , 25 m x = = = x 0 + v 0 x t 0 + 50 ( 0 , 5 ) 25 m Koordinat titik tertinggi ( 25 ; 101 , 25 ) m Peluru mencapai tanah saat y = 0 y 0 0 5 t 2 − 5 t − 100 t 2 − t − 20 ( t + 4 ) ( t − 5 ) t 1 = − 4 dan t 2 = 5 = = = = = = y 0 + v 0 t − 2 1 g t 2 100 + 5 ( t ) − 2 1 10 ( t ) 2 100 + 5 − 5 t 2 0 0 0 Jadi, peluru mencapai titik tertinggi setelah bergerak selama 0,5 s dan pada koordinat ( 25 ; 101 , 25 ) m , sedangkan mencapai tanah setelah bergerak 5 s.

Diketahui:

$v_{0 x} = 50 m / s$

$v_{0 y} = 5 m / s$

$y_{0} = 100 m$

$g = 10 m / s^{2}$

Ditanya: $t_{hma x}$ , koordinat $h_{ma x}$ , dan $t_{x ma x}$ ?

Pembahasan:

Saat mencapai titik tertinggi $v_{y} = 0$

$v_{y} 10 t t_{hma x} = = = = v_{0 y} - g t 5 - 10 t 5 0, 5 s$

Posisi saat mencapai titik tertinggi

$y = = = = y_{0} + v_{0 y} t - \frac{1}{2} g t^{2} 100 + 5 (0, 5) - \frac{1}{2} 10 (0, 5)^{2} 100 + 2, 5 - 1, 25 101, 25 m$

$x = = = x_{0} + v_{0 x} t 0 + 50 (0, 5) 25 m$

Koordinat titik tertinggi $(25; 101, 25) m$

Peluru mencapai tanah saat y = 0

$y 00 5 t^{2} - 5 t - 100 t^{2} - t - 20 (t + 4) (t - 5) t_{1} = - 4 dan t_{2} = 5 = = = = = = y_{0} + v_{0} t - \frac{1}{2} g t^{2} 100 + 5 (t) - \frac{1}{2} 10 (t)^{2} 100 + 5 - 5 t^{2} 000$

Jadi, peluru mencapai titik tertinggi setelah bergerak selama 0,5 s dan pada koordinat $(25; 101, 25) m$ , sedangkan mencapai tanah setelah bergerak 5 s.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

5.0 (2 rating)

Pertanyaan serupa

Sebuah bola dilempar dari tanah mendatar pada kecepatan awal 20 m/s pada sudut53°terhadap arah mendatar, seperti ditunjukkan pada gambar. Anggap gesekan udara dapat diabaikan. Tentukan: ke...

3.3

Jawaban terverifikasi

Bola dilemparkan dari sebuah gedung setinggi 7,5 m. Apabila kecepatan awal bola 20 m/s dan sudut elevasi bola 30°, tentukan: a. tinggi maksimum bola; b lama waktu bola di udara; c. jarak bola terja...

4.6

Jawaban terverifikasi

4.6

Jawaban terverifikasi

Sebuah bola dilempar dari tanah mendatar pada kecepatan awal 20 m/s pada sudut53°terhadap arah mendatar, seperti ditunjukkan pada gambar. Anggap gesekan udara dapat diabaikan. Tentukan: ke...

3.3

Jawaban terverifikasi

Buktikan secara matematis bahwa waktu yang digunakan untuk mencapai titik terjauh samadengan dua kali waktu yang digunakan untuk mencapai titik tertinggi!

4.0

Jawaban terverifikasi