Perhatikan gambar! Himpunan penyelesaian dari daerah yang diarsir adalah…

Pembahasan

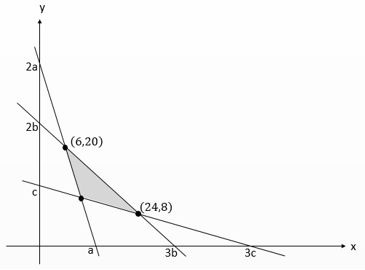
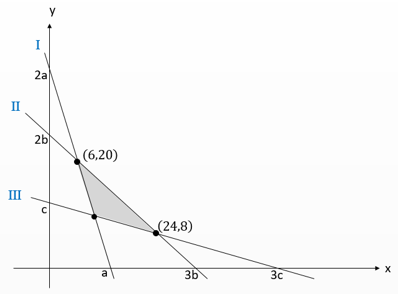
Perhatikan gambar Persamaan garis I adalah Subtitusi titik (6,20) 2 6 + 20 = 2 a 32 = 2 a a = 16 Maka persamaan garis I adalah 2 x + y = 2 16 ⇒ 2 x + y = 32 Untuk mencari daerah pertidaksamaan garis I, maka subtitusi titik (0,0) 2 0 + 0 … 32 0 … 32 Karena titik (0,0) berada di luar daerah pertidaksamaan garis I maka pertidaksamaan terakhir harus bernilai salah, berarti : 2 x + y ≥ 32 Persamaan garis II adalah Subtitusi titik (6,20) 2 6 + 3 20 = 6 b 72 = 6 b b = 12 Maka persamaan garis II adalah 2 x + 3 y = 6 12 ⇒ 2 x + 3 y = 72 Untuk mencari daerah pertidaksamaan garis I, maka subtitusi titik (0,0) 2 0 + 3 0 … 72 0 … 72 Karena titik (0,0) berada di dalam daerah pertidaksamaan garis II maka pertidaksamaan terakhir harus berniai salah, berarti : 2 x + 3 y ≤ 72 Persamaan garis III adalah Subtitusi titik (24,8) 24 + 3 8 = 3 c 48 = 3 c c = 16 Maka persamaan garis III adalah x + 3 y = 3 16 ⇒ x + 3 y = 48 Untuk mencari daerah pertidaksamaan garis III, maka subtitusi titik (0,0) 0 + 3 0 … 48 0 … 48 Karena titik (0,0) tidak berada di dalam daerah pertidaksamaan garis III maka pertidaksamaan terakhir harus berniai salah, berarti : x + 3 y ≥ 48 Maka himpunan pertidaksamaan adalah