Pertanyaan

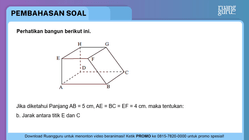
Perhatikan bangun berikut ini. Jika diketahui panjang AB = 5 cm , AE = BC = EF = 4 cm , maka tentukan: b. Jarak antara titik E dan C

Perhatikan bangun berikut ini.

Jika diketahui panjang $AB = 5 cm$ , $AE = BC = EF = 4 cm$ , maka tentukan:

b. Jarak antara titik E dan C

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

N. Puspita

Master Teacher

Jawaban terverifikasi

Jawaban

jarak antara titik E dan C adalah .

jarak antara titik E dan C adalah table attributes columnalign right center left columnspacing 0px end attributes row blank blank cell square root of 57 end cell end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank space end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank cm end table

table attributes columnalign right center left columnspacing 0px end attributes row blank blank cell square root of 57 end cell end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank space end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank cm end table

Pembahasan

Ingat! Jarak antar titik adalah lintasan terpendek yang ditarik lurus dari satu titik ke titik lainnya. Pada segitiga siku-siku berlaku teorema Pythagoras dengan adalah sisi siku-siku dan sisi miring. Diketahui prisma segi-4 ABCD.EFGH dengan panjang , . Seperti pada gambar berikut: Jarak antara titik A dan C adalah AC. Perhatikan segitiga ABC siku-siku di B, sehingga berlaku teorema Pythagoras sebagai berikut: Jarak antara titik E dan C adalah EC. Perhatikan segitiga ACE siku-siku di C seperti berikut: Segitiga ACE siku-siku di A, sehingga berlaku teorema Pythagoras sebagai berikut: Jadi, jarak antara titik E dan C adalah .

Ingat!

Jarak antar titik adalah lintasan terpendek yang ditarik lurus dari satu titik ke titik lainnya.
Pada segitiga siku-siku berlaku teorema Pythagoras dengan adalah sisi siku-siku dan sisi miring.

Diketahui prisma segi-4 ABCD.EFGH dengan panjang AB equals 5 space cm , AE equals BC equals EF equals 4 space cm . Seperti pada gambar berikut:

Jarak antara titik A dan C adalah AC. Perhatikan segitiga ABC siku-siku di B, sehingga berlaku teorema Pythagoras sebagai berikut:

table attributes columnalign right center left columnspacing 0px end attributes row AB equals cell square root of AB squared plus BC squared end root end cell row blank equals cell square root of 5 squared plus 4 squared end root end cell row blank equals cell square root of 25 plus 16 end root end cell row blank equals cell square root of 41 space cm end cell end table

Jarak antara titik E dan C adalah EC. Perhatikan segitiga ACE siku-siku di C seperti berikut:

Segitiga ACE siku-siku di A, sehingga berlaku teorema Pythagoras sebagai berikut:

Jadi, jarak antara titik E dan C adalah .

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.6 (68 rating)

Nazhwa sanica Zarin

Pembahasan lengkap banget Ini yang aku cari! Mudah dimengerti Makasih ❤️ Bantu banget

Nur Imaniar Naraya

Pembahasan lengkap banget

Putri Novita Toding Datu

Mudah dimengerti

Rika

Ini yang aku cari!

L Grim

Pembahasan lengkap banget Makasih ❤️

Pertanyaan serupa

Diketahui kubus ABCD.EFGH dengan panjang rusuk . Jika titik P terletak pada perpanjangan AB sehingga PB = 2 a , dan titik Q pada perpanjangan FG sehingga QG = a . a. Buatlah ilustrasi dari masalah ...

4.6

Jawaban terverifikasi

Kamar Akbar berbentuk balok dengan ukuran panjang : lebar : tinggi = 5 : 5 : 4. Di langit-langit kamar terdapat lampu yang letaknya tepat pada pusat bidang langit-langit. Pada salah satu dinding kamar...

323

4.6

Jawaban terverifikasi

Diketahui prisma tegak ABC . DEF dengan panjang AB = 26 cm , BC = 28 cm , dan AC = 30 cm . Jika tinggi prismanya 10 cm ,maka jarak antara titik E dengan titik C adalah ....cm

5.0

Jawaban terverifikasi

Perhatikan gambar kubus di samping! Jika titik P terletak di tengah rusuk CG, tentukan jarak antara titik A dan titik P!

4.4

Jawaban terverifikasi

Tentukan panjang LS dari kubus berikut.

5.0

Jawaban terverifikasi