Pertanyaan

Penyelesaian dari pertidaksamaan 8 lo g ( 2 1 lo g ( x 2 − 2 x x − 3 ) ) > 0 adalah ....

Penyelesaian dari pertidaksamaan $^{8} lo g (^{\frac{1}{2}} lo g (\frac{x - 3}{x ^{2} - 2 x})) > 0$ adalah ....

$x > 3$
$x < 0 atau 2 < x < 3$
$x < 0 atau x > 3$
$0 < x < 3$
$x < 0$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

N. Puspita

Master Teacher

Jawaban terverifikasi

Jawaban

jawaban yang benar adalah A.

Pembahasan

Ingat sifat pertidaksamaan logaritma berikut. untuk basis 0 < a < 1 , jika a lo g f ( x ) > a lo g g ( x ) maka f ( x ) < g ( x ) . Perhatikan penyelesaian berikut: 8 lo g ( 2 1 lo g ( x 2 − 2 x x − 3 ) ) 8 lo g ( 2 1 lo g ( x 2 − 2 x x − 3 ) ) 2 1 lo g ( x 2 − 2 x x − 3 ) 2 1 lo g ( x 2 − 2 x x − 3 ) x ( x − 2 ) x − 3 x ( x − 2 ) x − 3 − 2 1 2 x ( x − 2 ) 2 x − 6 − x 2 + 2 x 2 x ( x − 2 ) − x 2 + 4 x − 6 > > > > < < < < 0 8 lo g 1 1 2 1 lo g 2 1 2 1 0 0 0 Fungsi kuadrat − x 2 + 4 x − 6 mempunyai nilai D = − 8 < 0 . Sehingga − x 2 + 4 x − 6 definit negatif (selalu negatif). Maka berlaku: 2 x ( x − 2 ) > 0 . Diperoleh : x < 0 atau x > 2 .... (i) Syarat numerus 1: 2 1 lo g ( x 2 − 2 x x − 3 ) 2 1 lo g ( x 2 − 2 x x − 3 ) x 2 − 2 x x − 3 x 2 − 2 x x − 3 − 1 x 2 − 2 x x − 3 − x 2 + 2 x x ( x − 2 ) − x 2 + 3 x − 3 > > < < < < 0 2 1 lo g 1 1 0 0 0 Diperoleh − x 2 + 3 x − 3 definit negatif (selalu negatif). Maka berlaku: x ( x − 2 ) > ⇒ 0 x < 0 atau x > 2 .... (ii) Syarat Numerus 2: x 2 − 2 x x − 3 > 0 ⇒ x ( x − 2 ) x − 3 > 0 Pembuat nol: x = 0 , x = 2 , atau x = 3 Pada garis bilangan diperoleh: Diperoleh: 0 < x < 2 atau x > 3 (iii). 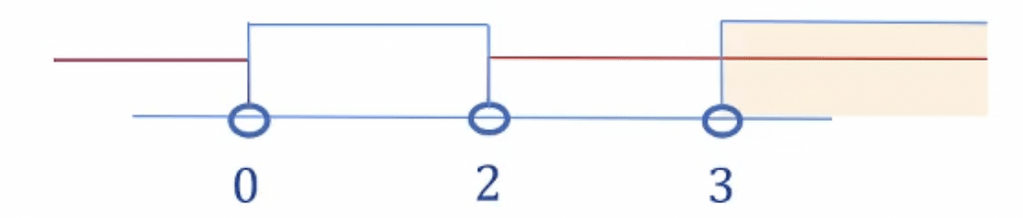Selanjutnya akan ditentukan daerah irisannya sebagai berikut Dengan demikian, dari pertidaksamaan (i), (ii), dan (iii) diperoleh irisan x > 3 . Oleh karena itu, jawaban yang benar adalah A.

Ingat sifat pertidaksamaan logaritma berikut.

untuk basis $0 < a < 1$ , jika $^{a} lo g f (x) >^{a} lo g g (x)$ maka $f (x) < g (x)$ .

Perhatikan penyelesaian berikut:

$^{8} lo g (^{\frac{1}{2}} lo g (\frac{x - 3}{x ^{2} - 2 x}))^{8} lo g (^{\frac{1}{2}} lo g (\frac{x - 3}{x ^{2} - 2 x}))^{\frac{1}{2}} lo g (\frac{x - 3}{x ^{2} - 2 x})^{\frac{1}{2}} lo g (\frac{x - 3}{x ^{2} - 2 x}) \frac{x - 3}{x ( x - 2 )} \frac{x - 3}{x ( x - 2 )} - \frac{1}{2} \frac{2 x - 6 - x ^{2} + 2 x}{2 x ( x - 2 )} \frac{- x ^{2} + 4 x - 6}{2 x ( x - 2 )} > > > > < < < < 0^{8} lo g 1 1^{\frac{1}{2}} lo g \frac{1}{2} \frac{1}{2} 000$

Fungsi kuadrat $- x^{2} + 4 x - 6$ mempunyai nilai $D = - 8 < 0$ . Sehingga $- x^{2} + 4 x - 6$ definit negatif (selalu negatif).

Maka berlaku: $2 x (x - 2) > 0$ .

Diperoleh : $x < 0$ atau $x > 2$ .... (i)

Syarat numerus 1:

$^{\frac{1}{2}} lo g (\frac{x - 3}{x ^{2} - 2 x})^{\frac{1}{2}} lo g (\frac{x - 3}{x ^{2} - 2 x}) \frac{x - 3}{x ^{2} - 2 x} \frac{x - 3}{x ^{2} - 2 x} - 1 \frac{x - 3 - x ^{2} + 2 x}{x ^{2} - 2 x} \frac{- x ^{2} + 3 x - 3}{x ( x - 2 )} > > < < < < 0^{\frac{1}{2}} lo g 1 1000$