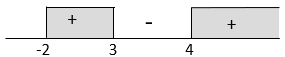Pertanyaan

Pak Rijal sedang mendesain animasi gambar yang melibatkan dua kurva berikut h ( x ) = x + 1 dan t ( x ) = x − 3 5 Pak Rijal menginginkan letak kurva h ( x ) di atas kurva t ( x ) . Batas-batas nilai x yang dibutuhkan Pak Rijal untuk mendesain gambar tersebut adalah ...

Pak Rijal sedang mendesain animasi gambar yang melibatkan dua kurva berikut

$h (x) = x + 1 dan t (x) = \frac{5}{x - 3}$

Pak Rijal menginginkan letak kurva $h (x)$ di atas kurva $t (x)$ . Batas-batas nilai $x$ yang dibutuhkan Pak Rijal untuk mendesain gambar tersebut adalah ...

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

N. Puspita

Master Teacher

Jawaban terverifikasi

Jawaban

Batas-batas nilai yang dibutuhkan Pak Rijal untuk mendesain gambar tersebut adalah .

Batas-batas nilai

yang dibutuhkan Pak Rijal untuk mendesain gambar tersebut adalah open curly brackets x vertical line minus 2 less than x less than 3 space atau space x greater than 4 comma space x element of R close curly brackets

open curly brackets x vertical line minus 2 less than x less than 3 space atau space x greater than 4 comma space x element of R close curly brackets

Pembahasan

Supaya letak kurva di atas kurva , maka haruslah . Dengan menyelesaikan pertidaksamaan tersebut diperoleh batas-batas nilai yang memenuhi, sebagai berikut Pembuat nol pembilang atau penyebut Uji titik Garis bilangan Jadi,Batas-batas nilai yang dibutuhkan Pak Rijal untuk mendesain gambar tersebut adalah .

Supaya letak kurva h left parenthesis x right parenthesis di atas kurva t left parenthesis x right parenthesis , maka haruslah h open parentheses x close parentheses greater than t open parentheses x close parentheses . Dengan menyelesaikan pertidaksamaan tersebut diperoleh batas-batas nilai yang memenuhi, sebagai berikut

$table attributes columnalign right center left columnspacing 0px end attributes row cell h open parentheses x close parentheses end cell greater than cell t open parentheses x close parentheses end cell row cell x plus 1 end cell greater than cell fraction numerator 5 over denominator x minus 3 end fraction end cell row cell x plus 1 minus fraction numerator 5 over denominator x minus 3 end fraction end cell greater than 0 row cell fraction numerator open parentheses x plus 1 close parentheses open parentheses x minus 3 close parentheses over denominator x minus 3 end fraction minus fraction numerator 5 over denominator x minus 3 end fraction end cell greater than 0 row cell fraction numerator x squared minus 2 x minus 3 over denominator x minus 3 end fraction minus fraction numerator 5 over denominator x minus 3 end fraction end cell greater than 0 row cell fraction numerator x squared minus 2 x minus 8 over denominator x minus 3 end fraction end cell greater than 0 end table$

Pembuat nol pembilang atau penyebut

Uji titik x equals 0 comma space

$fraction numerator open parentheses 0 close parentheses squared minus 2 open parentheses 0 close parentheses minus 8 over denominator open parentheses 0 close parentheses minus 3 end fraction equals fraction numerator negative 8 over denominator negative 3 end fraction equals 8 over 3 rightwards arrow positif$

Garis bilangan

open curly brackets x vertical line minus 2 less than x less than 3 space atau space x greater than 4 comma space x element of R close curly brackets

Jadi,Batas-batas nilai yang dibutuhkan Pak Rijal untuk mendesain gambar tersebut adalah open curly brackets x vertical line minus 2 less than x less than 3 space atau space x greater than 4 comma space x element of R close curly brackets .