Nilai x yang memenuhi persamaan adalah ....

Pembahasan

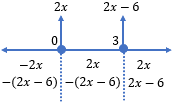
Dari soal diberikan persamaan . Akan dicari nilai-nilai yang memenuhi persamaan tersebut. Dimisalkan fungsi-fungsi sebagai berikut. Perhatikan masing-masing fungsi berikut! Untuk ,didapat nilai sebagai berikut. Untuk ,didapat nilai sebagai berikut. Perhatikan garis bilanganberikut! Berdasarkan gambar di atas, didapat tiga daerah, yaitu , , dan . Akan diperiksa hasil dari tiap daerah. Saat , didapat persamaan sebagai berikut. Perhatikan bahwa hanya terpenuhi apabila . Akan tetapi, nilai tidak memenuhi syarat . Akibatnya, bukanlah solusi dari persamaan . Jadi,tidak terdapat solusi dari persamaan nilai mutlak saat . Saat ,didapat persamaan sebagai berikut. Misalkan , makadidapat nilai sebagai berikut. Terlebih dahulu, akan dicari nilai yang berada padairisan antara interval dan ,yaitu . Perhatikan perhitungan berikut! Perhatikan bahwa tidak memenuhi , maka bukanlah solusi dari persamaan . Selanjutnya, akan dicari nilai yang berada pada irisan antara interval dan ,yaitu . Perhatikan perhitungan berikut! Perhatikan bahwa tidak memenuhi , maka bukanlah solusi dari persamaan . Jadi,tidak terdapat solusi dari persamaan nilai mutlak saat . Saat ,didapat persamaan sebagai berikut. Perhatikan bahwa hanya terpenuhi apabila .Akan tetapi, nilai tidak memenuhi syarat .Akibatnya, bukanlah solusi dari persamaan . Jadi,tidak terdapat solusi dari persamaan nilai mutlak saat . Dengan demikian, dapat disimpulkan bahwa tidak terdapat solusi dari persamaan untuk setiap bilangan real. Jadi, jawaban yang tepat adalah E.