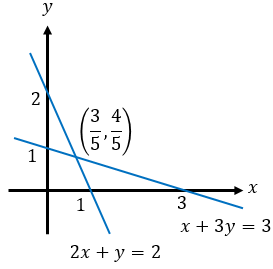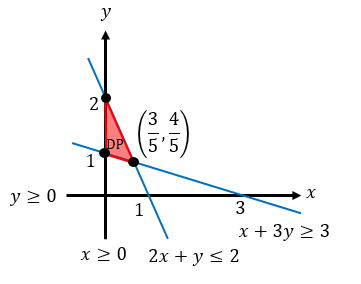Langkah-langkah mencari nilai optimum:
1. Gambar garis dan mencari titik potong kedua garis.
2. Menentukan daerah penyelesaian.
3. Menentukan nilai optimum.
Diketahui sistem pertidaksamaan  ;
;  ;
;  ; dan
; dan  dan fungsi objektif
dan fungsi objektif 
Penyelesaian:
1. Gambar garis dan mencari titik potong kedua garis.
Titik potong sumbu koordinat:
2x+y=2→(0,2) & (1,0)x+3y=3→(0,1) & (3,0)
Titik potong kedua garis:
2x+yy==22−2x
substitusi
x+3yx+3(2−2x)x+6−6x−5xx=====333−353
substistusi
yyyy====2−2x2−2⋅53510−5654
Didapat titik (53, 54).
Lalu gambar titik-titik yang dilalui sebagai berikut:
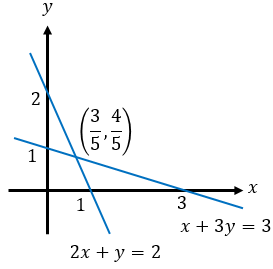
2. Menentukan daerah penyelesaian.
Untuk menentukan daerah penyelesaian perhatikan tabel berikut:
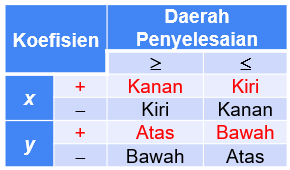
- Untuk 2x+y≤2 koefisien x positif dan ≤, maka daerah penyelesaian di sebelah kiri garis.
- Untuk x+3y≥3 koefisien x positif dan ≥, maka daerah penyelesaian di sebelah kanan garis.
- Untuk x≥0 koefisien x positif dan ≥, maka daerah penyelesaian di sebelah kanan garis.
- Untuk y≥0 koefisien x positif dan ≥, maka daerah penyelesaian di sebelah atas garis.
Daerah arsirannya sebagai berikut:
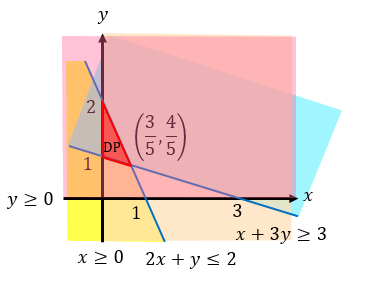
3. Menentukan nilai optimum.
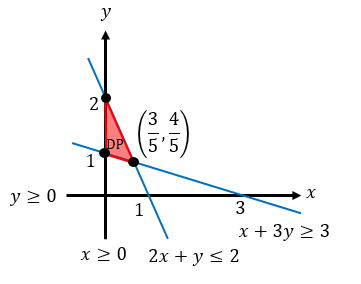
Dari gambar didapat titik-titik pojok (0, 1), (0, 2) dan (53, 54), lalu substitusikan ke fungsi objektif f(x,y)=3x+4y
f(0, 1)f(0, 2)f(53, 54)=====3(0)+4(1)=43(0)+4(2)=83(53)+4(54)59+5165
Jadi didapat nilai maksimum = 8.