Lakukan sekali lagi soal pada nomor (3) dengan menggunakan AB=c, AC=b, dan BC=a. Perlihatkan sekali lagi a2=b2+c2.

Pertanyaan

Lakukan sekali lagi soal pada nomor (3) dengan menggunakan $\text{AB}=c$ , $\mathrm{AC}=b$ , dan $\mathrm{BC}=a$ . Perlihatkan sekali lagi $a^2=b^2+c^2$ .

D. Rajib

Master Teacher

Mahasiswa/Alumni Universitas Muhammadiyah Malang

Jawaban terverifikasi

Jawaban

pada segitiga siku-siku berlaku hubungan $a^2=b^2+c^2$ dengan $a$ panjang sisi miring.

Pembahasan

Teorema Pythagoras menyatakan bahwa kuadrat panjang sisi miring suatu segitiga siku-siku sama dengan jumlah kuadrat panjang sisi-sisi lainnya. Secara sederhana dapat dirumuskan sebagai berikut.

$a^2=b^2+c^2$

dengan $a$ merupakan sisi miring (hipotenusa).

Ingat! Rumus luas bangun persegi adalah sebagai berikut.

${\text{L}}_\text{persegi}=s\times s$

Rumus luas segitiga adalah sebagai berikut.

${\text{L}}_\text{segitiga}=\frac12\times a\times t$

Gambar pada soal nomor 3 adalah sebagai berikut.

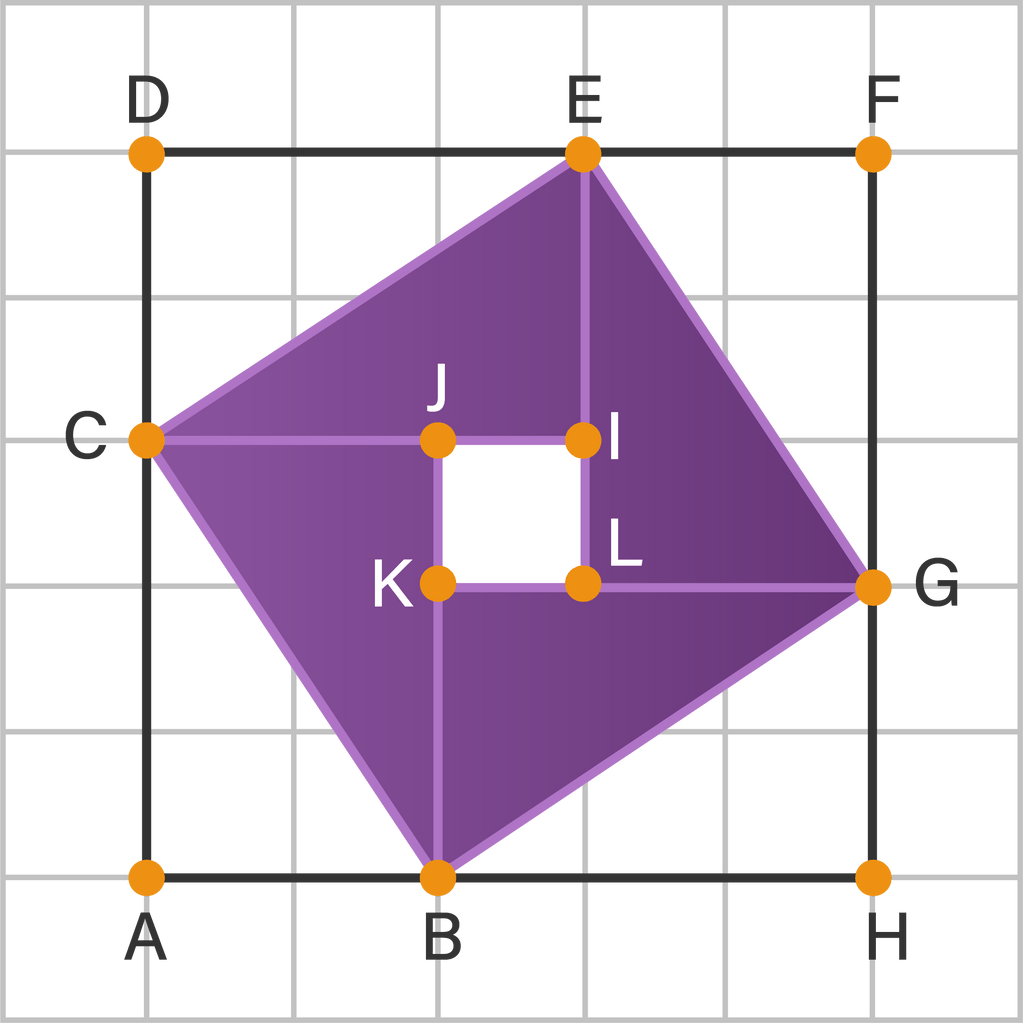
Luas masing-masing segitiga siku-siku tersebut dapat ditentukan sebagai berikut.

$table attributes columnalign right center left columnspacing 0px end attributes row cell text L end text subscript text BCJ end text end subscript end cell equals cell 1 half cross times text CJ end text cross times text BJ end text end cell row blank equals cell 1 half cross times c cross times b end cell row blank equals cell fraction numerator b c over denominator 2 end fraction end cell end table$

$table attributes columnalign right center left columnspacing 0px end attributes row cell text L end text subscript text BKG end text end subscript end cell equals cell 1 half cross times text BK end text cross times text KG end text end cell row blank equals cell 1 half cross times c cross times b end cell row blank equals cell fraction numerator b c over denominator 2 end fraction end cell end table$

$table attributes columnalign right center left columnspacing 0px end attributes row cell text L end text subscript text CEI end text end subscript end cell equals cell 1 half cross times text CI end text cross times text EI end text end cell row blank equals cell 1 half cross times b cross times c end cell row blank equals cell fraction numerator b c over denominator 2 end fraction end cell end table$

$table attributes columnalign right center left columnspacing 0px end attributes row cell text L end text subscript text ELG end text end subscript end cell equals cell 1 half cross times text LG end text cross times text EL end text end cell row blank equals cell 1 half cross times c cross times b end cell row blank equals cell fraction numerator b c over denominator 2 end fraction end cell end table$

Jadi, masing-masing segitiga mempunyai luas yang sama, yaitu $fraction numerator b c over denominator 2 end fraction$ satuan luas.

Panjang sisi persegi $\text{KLIJ}$ dapat ditentukan sebagai berikut.

$\begin{array}{rcl}\text{KL}&=&\text{KG}-\text{LG}\\&=&b-c\end{array}$

Luas persegi $\text{KLIJ}$ adalah sebagai berikut.

$\begin{array}{rcl}{\text{L}}_\text{KLIJ}&=&s\times s\\&=&\left(b-c\right)\left(b-c\right)\\&=&b^2-2bc+c^2\end{array}$

Luas persegi $\text{BGEC}$ dapat ditentukan sebagai berikut.

$table attributes columnalign right center left columnspacing 0px end attributes row cell text L end text subscript text BGEC end text end subscript end cell equals cell text L end text subscript text BCJ end text end subscript plus text L end text subscript text BKG end text end subscript plus text L end text subscript text CEI end text end subscript plus text L end text subscript text ELG end text end subscript plus text L end text subscript text KLIJ end text end subscript end cell row blank equals cell fraction numerator b c over denominator 2 end fraction plus fraction numerator b c over denominator 2 end fraction plus fraction numerator b c over denominator 2 end fraction plus fraction numerator b c over denominator 2 end fraction plus open parentheses b squared minus 2 b c plus c squared close parentheses end cell row blank equals cell fraction numerator 4 b c over denominator 2 end fraction plus open parentheses b squared minus 2 b c plus c squared close parentheses end cell row blank equals cell 2 b c plus open parentheses b squared minus 2 b c plus c squared close parentheses end cell row blank equals cell b squared plus c squared end cell end table$

Panjang sisi persegi $\text{BGEC}$ adalah $\text{BC}=a$ . Dengan menggunakan rumus luas persegi dapat ditentukan hubungan berikut.

$\begin{array}{rcl}{\text{L}}_\text{BGEC}&=&s\times s\\b^2+c^2&=&a\times a\\b^2+c^2&=&a^2\end{array}$

Dengan demikian, pada segitiga siku-siku berlaku hubungan $a^2=b^2+c^2$ dengan $a$ panjang sisi miring.

5.0 (1 rating)

Pertanyaan serupa

Ambillah empat lembar kertas. Tumpuk kertas-kertas tersebut. Buatlah segitiga siku-siku pada kertas paling atas, kemudian gunting tumpukan kertas tersebut sehingga menghasilkan empat segitiga siku-sik...

0.0

Jawaban terverifikasi

Pada kertas berpetak, buatlah segitiga siku-siku seperti gambar (i). Selanjutnya, dengan ukuran segitiga tersebut (dalam hal ini, ukuran sisi yang membentuk sudut 90∘ adalah 2 satuan dan 3 satuan), bu...

0.0

Jawaban terverifikasi

Susunlah 4 segitiga siku-siku seperti pada gambar. Perhatikan bahwa BGEC merupakan suatu persegi dengan ukuran BC. Perhatikan pula bahwa KLIJ merupakan persegi juga. Tentukan luas persegi BGEC melalui...

0.0

Jawaban terverifikasi

Hitunglah luas persegi-persegi berikut! a.

596

5.0

Jawaban terverifikasi

Hitunglah luas persegi-persegi berikut!

287

5.0

Jawaban terverifikasi