Pertanyaan

Perhatikan narasi berikut ini!

Batuan kuno yang mengandung ${}^{238}\mathrm U$ dapat ditentukan umurnya dengan menentukan umlah atom ${}^{206}\mathrm{Pb}$ dalam batuan tersebut. Metoda ini didasarkan pada peluruhan ${}^{238}\mathrm U$ menjadi ${}^{206}\mathrm{Pb}$ yang stabil. Hubungan antara jumlah atom ${}^{238}\mathrm U$ pada waktu t dengan jumlah semula ${\mathrm N}_0$ dapat diberikan oleh ${\mathrm N}_{\mathrm t}={\mathrm N}_0\times2^{-\frac{\mathrm t}{\mathrm p}}$ dengan p = waktu paruh. Hal ini diungkapkan dalam grafik:

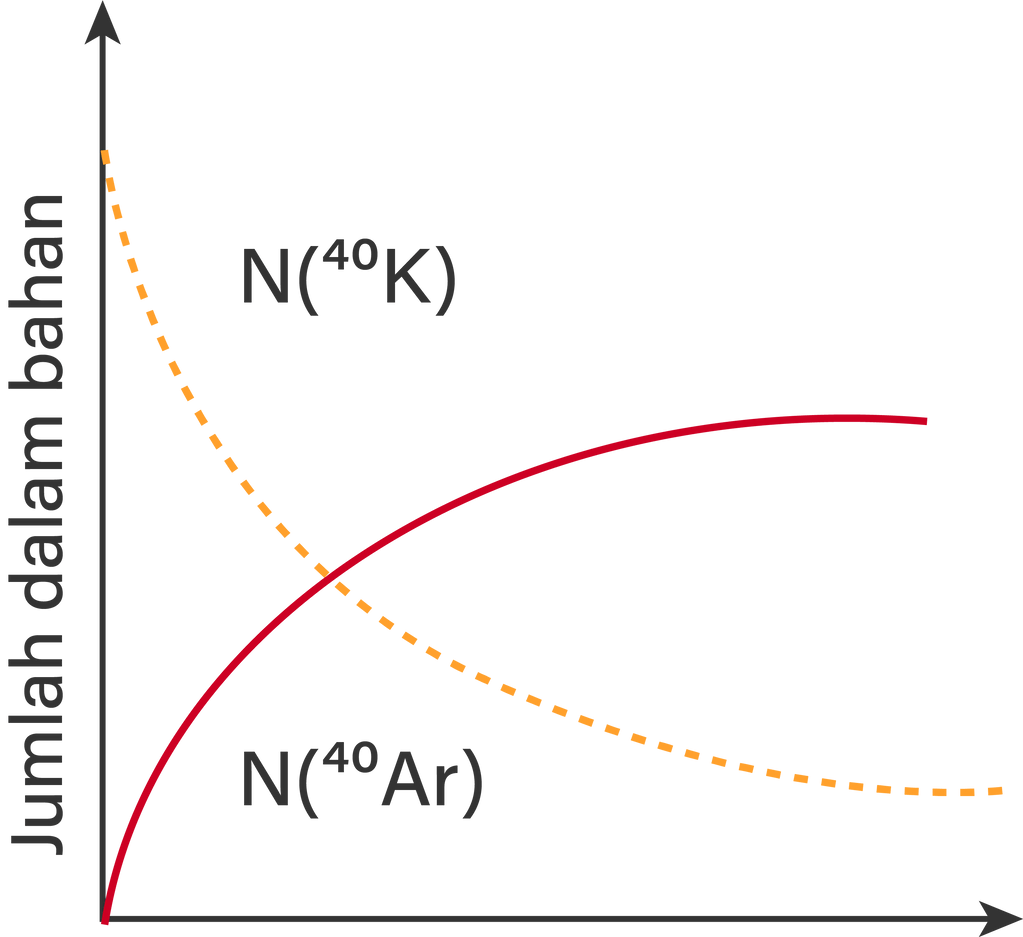
Waktu paruh ${}^{238}\mathrm U$ = 4,6 milyar tahun dan 1 milyar tahun = $10^9$ tahun. Cara lain yang dapat digunakan adalah dengan menentukan jumlah atom Ar dalam batuan sebagai hasil peluruhan ${}^{40}\mathrm K$ . Waktu paruh ${}^{40}\mathrm K$ adalah 1,3 milyar tahun. Dengan metoda ini para ahli geokimia menemukan bahwa umur batuan tertua di bumi adalah 3,8 milyar tahun.

Jumlah atom 238 U dalam batuan tertentu menyusut terhadap waktu secara ...

Jumlah atom $^{238} U$ dalam batuan tertentu menyusut terhadap waktu secara ... $\;$

linear
parabolik
hiperbolik
eksponensial
geometrik

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

B. Rohmawati

Master Teacher

Mahasiswa/Alumni Universitas Negeri Semarang

Jawaban terverifikasi

Jawaban

jumlah atom 238 U dalam batuan tertentu menyusut terhadap waktu secara eksponensial.

jumlah atom

^{238} U

dalam batuan tertentu menyusut terhadap waktu secara eksponensial.

Pembahasan

Jadi, jawaban yang benar adalah D. Peluruhan radioaktif adalah proses pemecahan inti atom yang tidak stabil sehingga terjadi kehilangan energi dengan memancarkan radiasi, seperti partikel alfa , partikel beta dengan neutrino dan sinar gamma . Peluruhan inti radioaktif (radionuklida) merupakan peristiwa statistik, oleh karena itu tidak bisa diperkirakan inti mana yang akan meluruh pada waktu berikutnya, tetapi untuk suatu kumpulan inti, dapat diperkirakan kebolehjadian terjadinya peluruhan.Secara matematis, jumlah peluruhan radionuklida per satuan waktu sebanding dengan hasil perkalian jumlah atom pada waktu tertentu dengan konstanta peluruhan. Persamaanpeluruhan suatu atom dituliskan sebagai berikut: N t = N 0 × 2 − p t Persamaan peluruhan atom tersebut merupakan persamaan eksponansial. Persamaan eksponensialadalahpersamaandari bilanganeksponendengan pangkat yang memuat sebuah fungsi, ataupersamaanperpangkatan yang bilangan pangkatnya mengandung variabel sebagai bilangan pengubah. Jadi, jumlah atom 238 U dalam batuan tertentu menyusut terhadap waktu secara eksponensial.

Jadi, jawaban yang benar adalah D.

Peluruhan radioaktif adalah proses pemecahan inti atom yang tidak stabil sehingga terjadi kehilangan energi dengan memancarkan radiasi, seperti partikel alfa, partikel beta dengan neutrino dan sinar gamma. Peluruhan inti radioaktif (radionuklida) merupakan peristiwa statistik, oleh karena itu tidak bisa diperkirakan inti mana yang akan meluruh pada waktu berikutnya, tetapi untuk suatu kumpulan inti, dapat diperkirakan kebolehjadian terjadinya peluruhan. Secara matematis, jumlah peluruhan radionuklida per satuan waktu sebanding dengan hasil perkalian jumlah atom pada waktu tertentu dengan konstanta peluruhan. Persamaan peluruhan suatu atom dituliskan sebagai berikut:

$N_{t} = N_{0} \times 2^{- \frac{t}{p}}$

Persamaan peluruhan atom tersebut merupakan persamaan eksponansial. Persamaan eksponensial adalah persamaan dari bilangan eksponen dengan pangkat yang memuat sebuah fungsi, atau persamaan perpangkatan yang bilangan pangkatnya mengandung variabel sebagai bilangan pengubah.

Jadi, jumlah atom $^{238} U$ dalam batuan tertentu menyusut terhadap waktu secara eksponensial.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

5.0 (1 rating)

Pertanyaan serupa

Dalam suatu batuan jumlah atom 40 K menjadi 8 1 jumlah semula dalam waktu .... (satuan miliar tahun)

5.0

Jawaban terverifikasi

Umur batuan yang saat ini mempunyai perbandingan 40 Ar terhadap 40 K sebesar 1:3 adalah ... tahun. (log 2 = 0,301; log 3 = 0,477)

5.0

Jawaban terverifikasi

Dalam suatu batuan jumlah atom 40 K menjadi 8 1 jumlah semula dalam waktu .... (satuan miliar tahun)

5.0

Jawaban terverifikasi

Umur batuan yang saat ini mempunyai perbandingan 40 Ar terhadap 40 K sebesar 1:3 adalah ... tahun. (log 2 = 0,301; log 3 = 0,477)

5.0

Jawaban terverifikasi

Untuk reaksi orde dua 2 A → B + C Molaritas mula-mula zat A = a M. Waktu paruh = 25 menit. a. Bagaimana susunan campuran setelah 50 menit? b. Setelah berapa menit campuran mengandung 30...

0.0

Jawaban terverifikasi