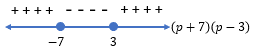Perhatikan perhitungan berikut!

Misalkan  , maka didapat hasil perhitungan sebagai berikut.
, maka didapat hasil perhitungan sebagai berikut.

Didapat pembuat nolnya adalah  atau
atau  .
.
Dengan melakukan uji titik pada tiap daerah, akan didapat garis bilangan sebagai berikut.
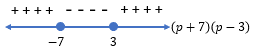
Karena tanda pertidaksamaannya adalah  , maka pilih daerah yang bernilai negatif atau nol, yaitu
, maka pilih daerah yang bernilai negatif atau nol, yaitu  .
.
Akibatnya, didapat pertidaksamaan sebagai berikut.

Karena  tidak mungkin bernilai negatif, maka pastilah terpenuhi
tidak mungkin bernilai negatif, maka pastilah terpenuhi  . Oleh karena itu, cukup perhatikan pertidaksamaan
. Oleh karena itu, cukup perhatikan pertidaksamaan  .
.
Berdasarkan definisi nilai mutlak, didapat bentuk sebagai berikut.

Untuk interval  , didapat hasil perhitungan sebagai berikut.
, didapat hasil perhitungan sebagai berikut.

Penyelesaian pada bagian ini adalah irisan dari  dan
dan  , yaitu
, yaitu  .
.
Untuk interval  , didapat hasil perhitungan sebagai berikut.
, didapat hasil perhitungan sebagai berikut.

Penyelesaian pada bagian ini adalah irisan dari  dan
dan  , yaitu
, yaitu  .
.
Jika kita gabungkan interval  dan
dan  , diperoleh daerah himpunan penyelesaian seperti pada garis bilangan berikut.
, diperoleh daerah himpunan penyelesaian seperti pada garis bilangan berikut.
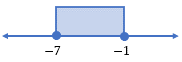
Dengan demikian, himpunan penyelesaian dari pertidaksamaan  adalah
adalah  .
.
Jadi, jawaban yang tepat adalah C.
adalah ....