Pertanyaan

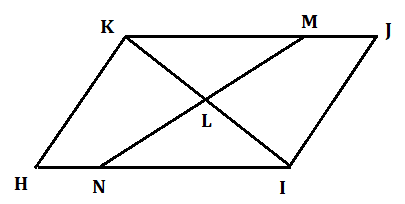
HIJK adalah jajargenjang. Titik L adalah titik tengahIK. Melalui titik L ditarik sebuah garis sembarang yang memotong HI di titik N dan memotong JK di titik M. Buktikan bahwa LM = LN!

HIJK adalah jajargenjang. Titik L adalah titik tengah IK. Melalui titik L ditarik sebuah garis sembarang yang memotong HI di titik N dan memotong JK di titik M. Buktikan bahwa LM = LN!

S. Indah

Master Teacher

Mahasiswa/Alumni Universitas Lampung

Jawaban terverifikasi

Jawaban

terbukti bahwaLM = LN.

terbukti bahwa LM = LN.

Pembahasan

Perhatikan gambar! dan kongruen, sebab: Syarat sudut-sudut-sudut terpenuhi, maka dan kongruen. Titik L merupakan titik tengah garis KI, maka KL = LI. Pasangan sisi yang sama panjang selain itu adalah KM danNI sertaLM danLN. Sehingga terbukti LM = LN. Dengan demikian, terbukti bahwaLM = LN.

Perhatikan gambar!

dan kongruen, sebab:

begin mathsize 14px style angle MKL equals angle NIL space left parenthesis sudut space dalam space berseberangan right parenthesis angle KML equals angle LNI space left parenthesis sudut space dalam space berseberangan right parenthesis angle KLM equals angle NLI space left parenthesis sudut space bertolak space belakang right parenthesis end style

Syarat sudut-sudut-sudut terpenuhi, maka dan kongruen.

Titik L merupakan titik tengah garis KI, maka KL = LI. Pasangan sisi yang sama panjang selain itu adalah KM dan NI serta LM dan LN. Sehingga terbukti LM = LN.

Dengan demikian, terbukti bahwa LM = LN.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

5.0 (1 rating)

Pertanyaan serupa

Ruang kelas sekolah Rogu terdiri dari 10 kelas dengan ukuran yang sama. Panjang, lebar dan tinggi kelas berturut-turut adalah 4 meter, 3 meter, 4 meter. Kemudian salah satu ruang kelas dibuatkan sebua...

5.0

Jawaban terverifikasi

Pada gambar berikut, bangun PQRS sebangundengan PQYX. Jika panjang PQ = 6 cm dan panjang QR = 9 cm , maka luas PQYXadalah ....

5.0

Jawaban terverifikasi

Lengkapi ... AB = AD ... = ... BE ! Bayangan gedung adalah BA = 12 m . Bayangan pohon CD adalah CA = 36 m .

0.0

Jawaban terverifikasi

Panjang SR adalah ... cm.

5.0

Jawaban terverifikasi

Perhatikan gambar sketsa kebun berikut. Sebidang kebun berbentuk jajargenjang. Pada bagian dalam kebun dibuat taman dengan panjang AB = 20 m dan panjang DE = 15 m . Di sekeliling taman akan dibu...

4.4

Jawaban terverifikasi