Gambarkan sketsa grafik fungsi berikut! f ( x ) = x 2 − 4 x − 5

Pembahasan

Untuk menentukan gambar dari fungsi kuadrat tersebut, perhatikan perhitungan berikut terlebih dahulu: Ingat kembali karakteristik fungsi kuadrat f ( x ) = a x 2 + b x + c dengan melihat nila : jika a > 0 maka grafiknya tebuka ke atas jika a < 0 maka grafiknya terbuka ke bawah Pada fungsi f ( x ) = x 2 − 4 x − 5 a = 1 , b = − 4 dan c = − 5 . terlihat bahwa a > 0 maka grafiknya terbuka ke atas. Titik potong sumbu x maka y = 0 f ( x ) y 0 0 x ​ = = = = = ​ x 2 − 4 x − 5 x 2 − 4 x − 5 x 2 − 4 x − 5 ( x − 5 ) ( x + 1 ) 5 atau x = − 1 ​ Diperoleh titik potong sumbu x adalah ( − 1 , 0 ) dan ( 5 , 0 ) Selanjutnya titik potong sumbu y maka x = 0 , sehingga: f ( x ) y y ​ = = = ​ x 2 − 4 x − 5 ( 0 ) 2 − 4 ( 0 ) − 5 − 5 ​ Diperoleh titik potong sumbu y adalah ( 0 , − 5 ) . Kemudian akan ditentukan titik puncak dari fungsi kuadrat tersebut. Ingat kembali rumus titik puncak: x p ​ = − 2 a b ​ y p ​ = − 4 a D ​ Pada fungsi f ( x ) = x 2 − 4 x − 5 , a = 1 , b = − 4 , c = − 5 . 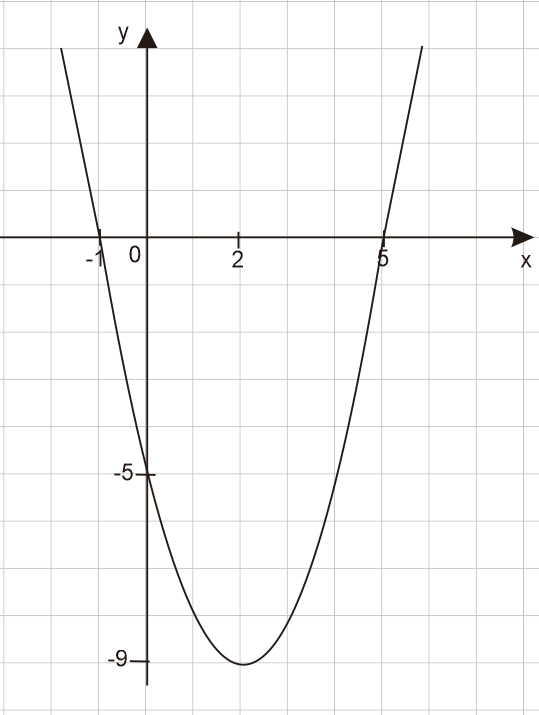Maka: x p ​ y p ​ ​ = = = = = = = = ​ − 2 a b ​ − 2 ( 1 ) ( − 4 ) ​ 2 − 4 a D ​ − 4 a b 2 − 4 a c ​ 4 ( 1 ) ( − 4 ) 2 − 4 ( 1 ) ( − 5 ) ​ − 4 16 + 20 ​ − 9 ​ Diperoleh titik puncaknya ( 2 , − 9 ) Diperoleh gambarnya: Dengan demikian, gambar dari fungsi kuadrat tersebut seperti gambar di atas.