Pertanyaan

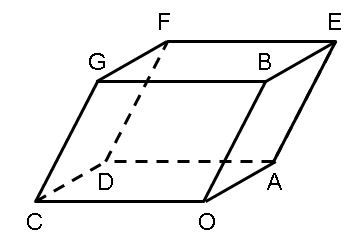
Gambar OADC.BEFG adalah paralelpipedum yaitu padatan dengan enam sisi. Setiap sisi jajargenjang yang berseberangan kongruen. O adalah titik asal. A, B, dan C masing-masing memiliki vektor posisi ⎝ ⎛ 1 0 0 ⎠ ⎞ , ⎝ ⎛ 2 1 2 ⎠ ⎞ , dan ⎝ ⎛ − 3 2 1 ⎠ ⎞ . Tunjukkan bahwa OF dan CE tegak lurus.

Gambar OADC.BEFG adalah paralelpipedum yaitu padatan dengan enam sisi. Setiap sisi jajargenjang yang berseberangan kongruen. O adalah titik asal. A, B, dan C masing-masing memiliki vektor posisi $⎝ ⎛ 100 ⎠ ⎞$ , $⎝ ⎛ 212 ⎠ ⎞$ , dan $⎝ ⎛ - 3 21 ⎠ ⎞$ .

Tunjukkan bahwa $OF$ dan $CE$ tegak lurus.

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

A. Salim

Master Teacher

Mahasiswa/Alumni Universitas Pelita Harapan

Jawaban terverifikasi

Jawaban

terbukti bahwa OF dan CE tegak lurus.

terbukti bahwa

OF

dan

CE

tegak lurus.

Pembahasan

Vektor posisi dari A, B, dan C dengan titik asal O dapat ditulis berturut-turut sebagai vektor OA = ⎝ ⎛ 1 0 0 ⎠ ⎞ , OB = ⎝ ⎛ 2 1 2 ⎠ ⎞ , dan vektor OC = ⎝ ⎛ − 3 2 1 ⎠ ⎞ . Dari gambar pada soal, diperoleh bahwa: OC = AD = BG = EF OB = AE = CD = DF OA = CD = BE = GF Vektor OF dan CE dapat diperoleh dengan menjumlahkan vektor sebagaimana perhitungan berikut: OF = = = = = OA + AE + EF OA + OB + OC ⎝ ⎛ 1 0 0 ⎠ ⎞ + ⎝ ⎛ 2 1 2 ⎠ ⎞ + ⎝ ⎛ − 3 2 1 ⎠ ⎞ ⎝ ⎛ 1 + 2 − 3 0 + 1 + 2 0 + 2 + 1 ⎠ ⎞ ⎝ ⎛ 0 3 3 ⎠ ⎞ CE = = = = = = CD + DA + AE OA − AD + OB OA − OC + OB ⎝ ⎛ 1 0 0 ⎠ ⎞ − ⎝ ⎛ − 3 2 1 ⎠ ⎞ + ⎝ ⎛ 2 1 2 ⎠ ⎞ ⎝ ⎛ 1 − ( − 3 ) + 2 0 − 2 + 1 0 − 1 + 2 ⎠ ⎞ ⎝ ⎛ 6 − 1 1 ⎠ ⎞ Dua vektor dapat dikatakan saling tegak lurus apabila hasil kali dot product kedua vektor tersebut memberikan nilai nol. Ingat bahwa hasil kali dot product dari vektor a = ⎝ ⎛ a 1 a 2 a 3 ⎠ ⎞ dan b = ⎝ ⎛ b 1 b 2 b 3 ⎠ ⎞ dapat dirumuskan sebagai berikut: a ⋅ b = a 1 b 1 + a 2 b 2 + a 3 b 3 Sehingga, OF ⋅ CE = = = ⎝ ⎛ 0 3 3 ⎠ ⎞ ⋅ ⎝ ⎛ 6 − 1 1 ⎠ ⎞ ( 0 ) ( 6 ) + ( 3 ) ( − 1 ) + ( 3 ) ( 1 ) 0 Karena hasil kali dot product antara OF dan CE bernilai nol, maka OF dan CE saling tegak lurus. Dengan demikian, terbukti bahwa OF dan CE tegak lurus.

Vektor posisi dari A, B, dan C dengan titik asal O dapat ditulis berturut-turut sebagai vektor $OA = ⎝ ⎛ 100 ⎠ ⎞$ , $OB = ⎝ ⎛ 212 ⎠ ⎞$ , dan vektor $OC = ⎝ ⎛ - 3 21 ⎠ ⎞$ .

Dari gambar pada soal, diperoleh bahwa:

$OC = AD = BG = EF OB = AE = CD = DF OA = CD = BE = GF$

Vektor $OF$ dan $CE$ dapat diperoleh dengan menjumlahkan vektor sebagaimana perhitungan berikut:

$OF = = = = = OA + AE + EF OA + OB + OC ⎝ ⎛ 100 ⎠ ⎞ + ⎝ ⎛ 212 ⎠ ⎞ + ⎝ ⎛ - 3 21 ⎠ ⎞ ⎝ ⎛ 1 + 2 - 3 0 + 1 + 2 0 + 2 + 1 ⎠ ⎞ ⎝ ⎛ 033 ⎠ ⎞$

$CE = = = = = = CD + DA + AE OA - AD + OB OA - OC + OB ⎝ ⎛ 100 ⎠ ⎞ - ⎝ ⎛ - 3 21 ⎠ ⎞ + ⎝ ⎛ 212 ⎠ ⎞ ⎝ ⎛ 1 - (- 3) + 2 0 - 2 + 1 0 - 1 + 2 ⎠ ⎞ ⎝ ⎛ 6 - 1 1 ⎠ ⎞$

Dua vektor dapat dikatakan saling tegak lurus apabila hasil kali dot product kedua vektor tersebut memberikan nilai nol.

Ingat bahwa hasil kali dot product dari vektor $a = ⎝ ⎛ a_{1} a_{2} a_{3} ⎠ ⎞$ dan $b = ⎝ ⎛ b_{1} b_{2} b_{3} ⎠ ⎞$ dapat dirumuskan sebagai berikut:

$a \cdot b = a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}$

Sehingga,

$OF \cdot CE = = = ⎝ ⎛ 033 ⎠ ⎞ \cdot ⎝ ⎛ 6 - 1 1 ⎠ ⎞ (0) (6) + (3) (- 1) + (3) (1) 0$

Karena hasil kali dot product antara $OF$ dan $CE$ bernilai nol, maka $OF$ dan $CE$ saling tegak lurus.

Dengan demikian, terbukti bahwa $OF$ dan $CE$ tegak lurus.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

0.0 (0 rating)

Pertanyaan serupa

Diketahui vektor a = i + 2 j − x k , b = 3 i − 2 j + k , dan c = 2 i + j + 2 k . Jika a tegak lurus c , maka ( c + b ) ⋅ ( a − c ) adalah ....

4.6

Jawaban terverifikasi

Diketahui vektor a = i + 2 j − x k , b = 3 i − 2 j + k , dan c = 2 i + j + 2 k . Jika a tegak lurus c , maka ( c + b ) ⋅ ( a − c ) adalah ....

4.6

Jawaban terverifikasi

Diketahui vektor a = 6 x i + 2 x j − 8 k , b = − 4 i + 8 j + 10 k , dan c = − 2 i + 3 j − 5 k . Jika a dan b tegak lurus, vektor ( a − c ) adalah ....

5.0

Jawaban terverifikasi

Diketahui vektor a = 2 t i − j + 3 k , b = − t i + 2 j − 5 k , dan c = 3 t i + t j + k . Jika vektor ( a + b ) tegak lurus c , maka nilai 2 t = ....

4.5

Jawaban terverifikasi

Diketahui vektor a = 6 x i + 2 x j − 8 k , b = − 4 i + 8 j + 10 k , dan c = − 2 i + 3 j − 5 k . Jika a dan b tegak lurus, vektor ( a − c ) adalah ....

5.0

Jawaban terverifikasi