Iklan
Pertanyaan
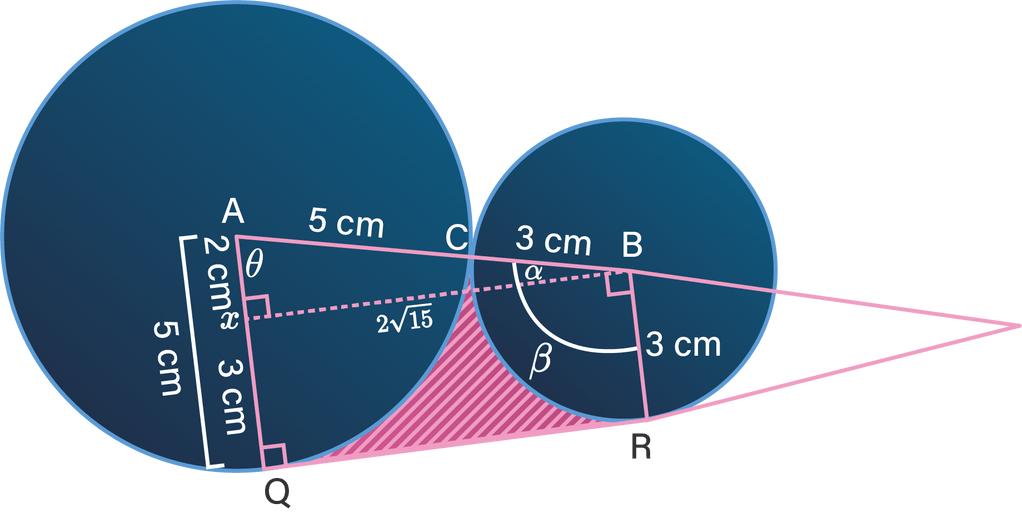
Gambar berikut menunjukkan dua lingkaran yang bersinggungan di C dan berpusat di A dan B . Jika panjang AC dan BC masing-masing 5 cm dan 3 cm , serta PQ ialah garis singgung sekutu pada titik Q dan R , maka luas daerah arsiran adalah ....
Gambar berikut menunjukkan dua lingkaran yang bersinggungan di dan berpusat di dan .
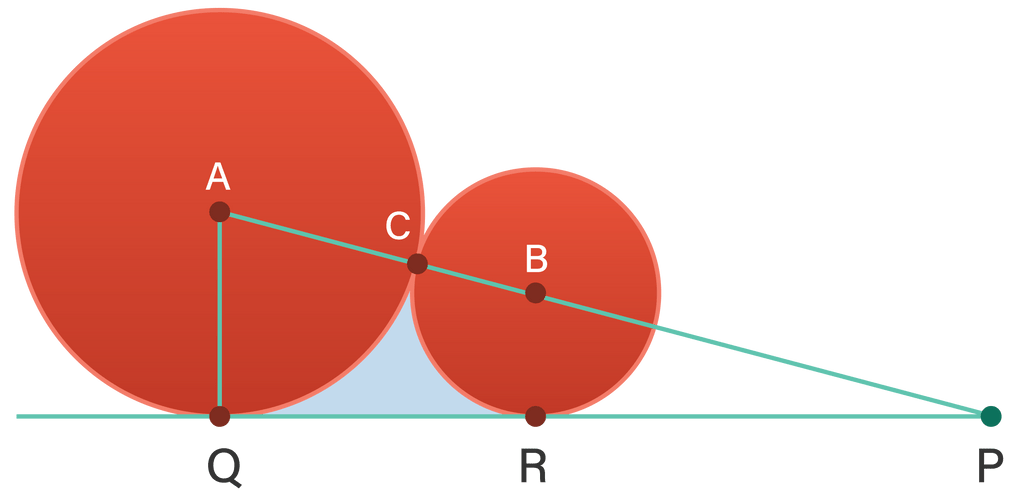
Jika panjang dan masing-masing dan , serta ialah garis singgung sekutu pada titik dan , maka luas daerah arsiran adalah ....
Iklan
DR
D. Rajib
Master Teacher
Mahasiswa/Alumni Universitas Muhammadiyah Malang
Jawaban terverifikasi
9
5.0 (1 rating)
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2025 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia