Diketahui f(x)=sin2 2x untuk 0≤x≤π. Tentukan interval fungsi f(x) naik dan interval fungsi turun.

Pertanyaan

Diketahui $f(x)=\sin^2\;2x$ untuk $0\leq x\leq\mathrm\pi$ . Tentukan interval fungsi $f(x)$ naik dan interval fungsi f left parenthesis x right parenthesis turun.

E. Lestari

Master Teacher

Mahasiswa/Alumni Universitas Sebelas Maret

Jawaban terverifikasi

Jawaban

disimpulkan interval naik pada fungsi $f$ adalah $0 less or equal than x less than straight pi over 4 space atau space straight pi over 2 less than straight x less than fraction numerator 3 straight pi over denominator 4 end fraction$ sementara interval turun fungsi $f$ adalah $straight pi over 4 less than x less than straight pi over 2 space atau space fraction numerator 3 straight pi over denominator 4 end fraction less than straight x less or equal than straight pi$ .

Pembahasan

Fungsi $f$ naik ketika $f'(x)>0$ dan turun ketika $f'(x)<0$ . Maka dari itu, untuk menjawab soal di atas kita perlu mencari turunan dari fungsi $f$ menggunakan aturan rantai berikut ini:

$f apostrophe left parenthesis x right parenthesis equals fraction numerator straight d a over denominator straight d b end fraction times fraction numerator straight d b over denominator straight d c end fraction times fraction numerator straight d c over denominator straight d x end fraction$

Diberikan fungsi f left parenthesis x right parenthesis equals sin squared space 2 x , maka kita misalkan menjadi:

$\begin{array}{rcl}a&=&b^2\\b&=&\sin\;c\\c&=&2x\end{array}$

Pertama cari turunan dari $a$ dengan:

$table attributes columnalign right center left columnspacing 0px end attributes row a equals cell b squared end cell row cell fraction numerator straight d a over denominator straight d b end fraction end cell equals cell 2 b end cell end table$

Lalu cari turunan $b$ yaitu:

$table attributes columnalign right center left columnspacing 0px end attributes row b equals cell sin space c space end cell row cell fraction numerator straight d b over denominator straight d c end fraction end cell equals cell cos space c end cell end table$

terakhir cari turunan dari $c$ yaitu:

$table attributes columnalign right center left columnspacing 0px end attributes row c equals cell 2 x end cell row cell fraction numerator straight d c over denominator straight d x end fraction end cell equals 2 end table$

Setelah ketiganya diturunkan, maka turunan dari $f(x)$ adalah

$table attributes columnalign right center left columnspacing 0px end attributes row cell f apostrophe left parenthesis x right parenthesis end cell equals cell fraction numerator straight d a over denominator straight d b end fraction times fraction numerator straight d b over denominator straight d c end fraction times fraction numerator straight d c over denominator straight d x end fraction end cell row blank equals cell 2 b times cos space c times 2 end cell row blank equals cell 4 b space cos space c end cell row blank equals cell 4 space sin space c space cos space c end cell row blank equals cell 4 space sin space 2 x space cos space 2 x end cell row blank equals cell 2 times bold 2 bold space bold italic s bold italic i bold italic n bold 2 bold italic x bold space bold italic c bold italic o bold italic s bold space bold 2 bold italic x end cell row blank equals cell 2 space bold italic s bold italic i bold italic n bold space bold 2 bold left parenthesis bold 2 bold italic x bold right parenthesis end cell row blank equals cell 2 space sin space 4 x end cell end table$

Persamaan di atas yang ditebalkan menggunakan identitas trigonometri $2\;\sin\;\alpha\;\cos\;\alpha=\sin\;2\alpha$

Dari hasil diatas, diperoleh $f'(x)=2\;\sin\;4x$ , maka selanjutnya adalah buat titik pembuat $0$ nya dengan cara berikut ini:

$\begin{array}{rcl}f'(x)&=&0\\2\;\sin\;4x&=&0\\\sin\;4x&=&0\;\end{array}$

Gunakan persamaan trigonometri untuk mempelroh nilai $x$ pembuat nol nya yaitu:

$\begin{array}{rcl}\sin\;4x&=&0\\\sin\;4x&=&\sin\;0\;\\&&\\x_1&=&\alpha+k\cdot2\mathrm\pi\;\;\;\;\;\mathrm{atau}\;\;\;\;{\mathrm x}_2=\mathrm\pi-\mathrm\alpha+\mathrm k\cdot2\mathrm\pi\\4\mathrm x&=&0+\mathrm k\cdot2\mathrm\pi\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;4\mathrm x=\mathrm\pi-0+\mathrm k\cdot2\mathrm\pi\\&&\mathrm{selanjunya}\;\mathrm{bagi}\;4,\;\mathrm{diperoleh}\;\\\mathrm x&=&0+\mathrm k\cdot\frac{\mathrm\pi}2\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm x=\frac{\mathrm\pi}4+\mathrm k\cdot\frac{\mathrm\pi}2\end{array}$

Setelah itu kita subtitusikan $k$ nya dengan bilangan bulat yang memenuhi batas interval $0\leq x\leq\mathrm\pi$ yaitu:

$\begin{array}{rcl}\mathrm x&=&0+\mathrm k\cdot\frac{\mathrm\pi}2\\k&=&{0\rightarrow x=0+0\cdot\frac{\mathrm\pi}2=0+0=0}\\k&=&{1\rightarrow x=0+1\cdot\frac{\mathrm\pi}2=0+\frac{\mathrm\pi}2=\frac{\mathrm\pi}2}\\k&=&{2\rightarrow x=0+2\cdot\frac{\mathrm\pi}2=0+\mathrm\pi=\mathrm\pi}\end{array}$

Lalu substitusikan juga pada $x_2$ yaitu:

$table attributes columnalign right center left columnspacing 0px end attributes row straight x equals cell straight pi over 4 plus straight k times straight pi over 2 end cell row k equals cell 0 rightwards arrow x equals straight pi over 4 plus 0 times straight pi over 2 equals straight pi over 4 plus 0 equals straight pi over 4 end cell row k equals cell 1 rightwards arrow x equals straight pi over 4 plus 1 times straight pi over 2 equals straight pi over 4 plus straight pi over 2 equals fraction numerator 3 straight pi over denominator 4 end fraction end cell end table$

Maka diperoleh titik pembuat nol nya yaitu: $0 comma straight pi over 4 comma straight pi over 2 comma fraction numerator 3 straight pi over denominator 4 end fraction space dan space straight pi$ . Setelah itu, dibuat diagram garis di bawah ini kemudian lakukan uji titik untuk menentukan daerah $+$ dan $-$ nya. Sehingga diperoleh diagram garis di bawah ini:

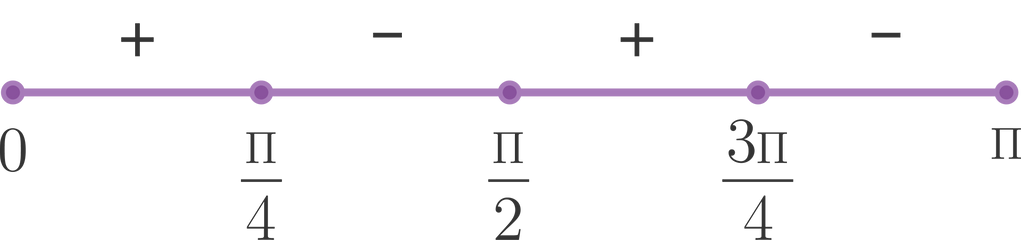
Dengan demikian, disimpulkan interval naik pada fungsi $f$ adalah $0 less or equal than x less than straight pi over 4 space atau space straight pi over 2 less than straight x less than fraction numerator 3 straight pi over denominator 4 end fraction$ sementara interval turun fungsi $f$ adalah $straight pi over 4 less than x less than straight pi over 2 space atau space fraction numerator 3 straight pi over denominator 4 end fraction less than straight x less or equal than straight pi$ .