Pertanyaan

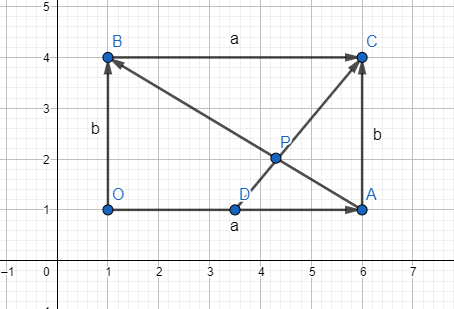
Diketahui persegi panjang OACB , D titiktengah OA , dan P titik potong CD dengandiagonal AB . Jika a = OA dan b = OB ,tentukan: a. CP b. OP c. BP d. AP e. DP

Diketahui persegi panjang $OACB$ , $D$ titik tengah $OA$ , dan $P$ titik potong $CD$ dengan diagonal $AB$ . Jika $a = OA$ dan $b = OB$ , tentukan:

a. $CP$
b. $OP$
c. $BP$
d. $AP$
e. $DP$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

Z. Apriani

Master Teacher

Mahasiswa/Alumni Institut Teknologi Bandung

Jawaban terverifikasi

Pembahasan

Jawaban yang benar untuk pertanyaan tersebut adalah a. CP → = − 3 1 ( a + 2 b ) , b. OP → = 3 1 ( 2 a + b ) , c. BP → = 3 2 ( a − b ) , d. AP → = − 3 1 ( a − b ) , e. DP → = 6 1 ( a + 2 b ) . Ingat bahwa resultan dua vektor a dan b berikut: c = a + b Ingat pula bahwa vektor a yang saling sejajar dengan vektor b berikut: a = b Dan vektor a yang berlawanan arah dengan vektor b berikut: a = − b Berdasarkan rumus dan informasi di atas, maka persoalan tersebut dapat digambarkan sebagai berikut: Vektor CP dapat dinyatakan sebagai berikut: CP = 3 2 CD Dimana CD = − DC dan DC = 2 1 a + b , sehingga vektor CP dapat ditentukan sebagai berikut: CP = = = = 3 2 CD − 3 2 DC − 3 2 ( 2 1 a + b ) − 3 1 ( a + 2 b ) Vektor OP dapat dinyatakan sebagai berikut: OP = OD + DP Dimana OD = 2 1 a dan DP = 3 1 DC = 3 1 ( 2 1 a + b ) sehingga vektor OP dapat ditentukan sebagai berikut: OP = = = = = OD + DP 2 1 a + 3 1 ( 2 1 a + b ) 2 1 a + 6 1 a + 3 1 b 6 4 a + 3 1 b 3 1 ( 2 a + b ) Vektor BP dapat dinyatakan sebagai berikut: BP = 3 2 BA Dimana BA = − b + a , sehingga vektor BP dapat ditentukan sebagai berikut: BP = = = 3 2 BA 3 2 ( − b + a ) 3 2 ( a − b ) Vektor AP dapat dinyatakan sebagai berikut: AP = 3 1 AB Dimana AB = − a + b sehingga vektor AP dapat ditentukan sebagai berikut: AP = = = 3 1 AB 3 1 ( − a + b ) − 3 1 ( a − b ) Vektor DP dapat dinyatakan sebagai berikut: DP = 3 1 DC Dimana DC = 2 1 a + b sehingga vektor DP ditentukan sebagai berikut: DP = = = 3 1 DC 3 1 ( 2 1 a + b ) 6 1 ( a + 2 b ) Dengan demikian, maka: a. CP = − 3 1 ( a + 2 b ) , b. OP = 3 1 ( 2 a + b ) , c. BP = 3 2 ( a − b ) , d. AP = − 3 1 ( a − b ) , e. DP = 6 1 ( a + 2 b ) .

Jawaban yang benar untuk pertanyaan tersebut adalah

a. $CP \to = - \frac{1}{3} (a + 2 b)$ ,

b. $OP \to = \frac{1}{3} (2 a + b)$ ,

c. $BP \to = \frac{2}{3} (a - b)$ ,

d. $AP \to = - \frac{1}{3} (a - b)$ ,

e. $DP \to = \frac{1}{6} (a + 2 b)$ .

Ingat bahwa resultan dua vektor $a$ dan $b$ berikut:

$c = a + b$

Ingat pula bahwa vektor $a$ yang saling sejajar dengan vektor $b$ berikut:

$a = b$

Dan vektor $a$ yang berlawanan arah dengan vektor $b$ berikut:

$a = - b$

Berdasarkan rumus dan informasi di atas, maka persoalan tersebut dapat digambarkan sebagai berikut:

Vektor $CP$ dapat dinyatakan sebagai berikut:

$CP = \frac{2}{3} CD$

Dimana $CD = - DC$ dan $DC = \frac{1}{2} a + b$ , sehingga vektor $CP$ dapat ditentukan sebagai berikut:

$CP = = = = \frac{2}{3} CD - \frac{2}{3} DC - \frac{2}{3} (\frac{1}{2} a + b) - \frac{1}{3} (a + 2 b)$

Vektor $OP$ dapat dinyatakan sebagai berikut:

$OP = OD + DP$

Dimana $OD = \frac{1}{2} a$ dan $DP = \frac{1}{3} DC = \frac{1}{3} (\frac{1}{2} a + b)$ sehingga vektor $OP$ dapat ditentukan sebagai berikut:

$OP = = = = = OD + DP \frac{1}{2} a + \frac{1}{3} (\frac{1}{2} a + b) \frac{1}{2} a + \frac{1}{6} a + \frac{1}{3} b \frac{4}{6} a + \frac{1}{3} b \frac{1}{3} (2 a + b)$

Vektor $BP$ dapat dinyatakan sebagai berikut:

$BP = \frac{2}{3} BA$

Dimana $BA = - b + a$ , sehingga vektor $BP$ dapat ditentukan sebagai berikut:

$BP = = = \frac{2}{3} BA \frac{2}{3} (- b + a) \frac{2}{3} (a - b)$

Vektor $AP$ dapat dinyatakan sebagai berikut:

$AP = \frac{1}{3} AB$

Dimana $AB = - a + b$ sehingga vektor $AP$ dapat ditentukan sebagai berikut:

$AP = = = \frac{1}{3} AB \frac{1}{3} (- a + b) - \frac{1}{3} (a - b)$

Vektor $DP$ dapat dinyatakan sebagai berikut:

$DP = \frac{1}{3} DC$

Dimana $DC = \frac{1}{2} a + b$ sehingga vektor $DP$ ditentukan sebagai berikut:

$DP = = = \frac{1}{3} DC \frac{1}{3} (\frac{1}{2} a + b) \frac{1}{6} (a + 2 b)$

Dengan demikian, maka:

a. $CP = - \frac{1}{3} (a + 2 b)$ ,

b. $OP = \frac{1}{3} (2 a + b)$ ,

c. $BP = \frac{2}{3} (a - b)$ ,

d. $AP = - \frac{1}{3} (a - b)$ ,

e. $DP = \frac{1}{6} (a + 2 b)$ .

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.5 (16 rating)

ainun salwa nisa

Ini yang aku cari!

Pertanyaan serupa

Diketahui titik A(-2,1) terletak pada garis dengan persamaan 2x+5y=1. Persamaan vektor dari garis tersebut dengan titik acuan pada titik A adalah ....

0.0

Jawaban terverifikasi

Perhatikan gambar berikut Diketahui garis l adalah garis yang melalui titik A dan sejajar dengan vektor p .Diketahui pula garis l melalui titik R. Jika a dan r masing-masing adalah vektor posi...

5.0

Jawaban terverifikasi

Pada kubus PQRS . TUVW , dapat ditentukan bahwa: SV − WU + WQ = ...

4.8

Jawaban terverifikasi

Pada balok ABCD . EFGH , dapat ditentukan bahwa: AB − AD + AH = ...

4.8

Jawaban terverifikasi

Diketahui segi enam beraturan ABCDEF .Jika AB = u dan AF = v , tentukan AB + AC + AD + AE + AF dalam u dan v .

4.3

Jawaban terverifikasi