Diketahui persamaan kuadrat mx−(2m+1)x+m+5=0 memiliki akar-akar real. Akibatnya, nilai diskriminan dari persamaan kuadrat tersebut akan lebih besar atau sama dengan 0.
Perhatikan perhitungan berikut!
Db2−4ac(−(2m+1))2−4⋅m⋅(m+5)4m2+4m+1−4m2−20m1−16m116m1616mm≥≥≥≥≥≥≤≤≤0000016m1161161
Didapat m≤161 dan penyelesaian tersebut dapat kita tuliskan sebagai penyelesaian pertama, yaitu m≤161 … (i).
Kemudian, diketahui pula bahwa nilai akar-akar persamaan kuadrat tersebut tidak kurang dari −3. Akibatnya, x1≥−3 dan x2≥−3, atau dapat juga dituliskan x1+3≥0 dan x2+3≥0. Dengan menggunakan rumus jumlah akar dan hasil kali akar, didapat batasan nilai m lainnya adalah sebagai berikut.
- Jumlah dari x1+3 dan x2+3
Karena x1+3≥0 dan x2+3≥0, maka hasil penjumlahan keduanya akan lebih besar atau sama dengan 0. Oleh karena itu, didapat batasan nilai m sebagai berikut.
(x1+3)+(x2+3)x1+x2+6−ab+6−m−(2m+1)+6m2m+1+m6mm8m+1m≤−81 atau m≥≥≥≥≥≥>0000000
Didapat m≤−81 atau m>0 dan penyelesaian tersebut dapat kita tuliskan sebagai penyelesaian kedua, yaitu m≤-81 atau m>0 … (ii).
- Hasil kali dari x1+3 dan x2+3
Karena x1+3≥0 dan x2+3≥0, maka hasil kali keduanya akan lebih besar atau sama dengan 0. Oleh karena itu, didapat batasan nilai m sebagai berikut.
(x1+3)⋅(x2+3)x1⋅x2+3x1+3x2+9x1⋅x2+3(x1+x2)+9ac+3(−ab)+9mm+5+3(−m−(2m+1))+9mm+5+3(m2m+1)+9mm+5+m6m+3+m9mm16m+8m≤−21 atau m≥≥≥≥≥≥≥≥≥000000000
Didapat m≤−21 atau m>0 dan penyelesaian tersebut dapat kita tuliskan sebagai penyelesaian ketiga, yaitu m≤-21 atau m>0 … (iii).
Batasan nilai-nilai m yang memenuhi merupakan hasil irisan dari penyelesaian (i), (ii), dan (iii) sebagai berikut.
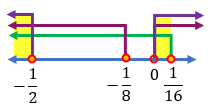
Dengan demikian, batasan nilai-nilai m yang memenuhi adalah {m∣ m≤−21 atau 0<m≤−161}.
Jadi, jawaban yang tepat adalah C.
















