Pertanyaan

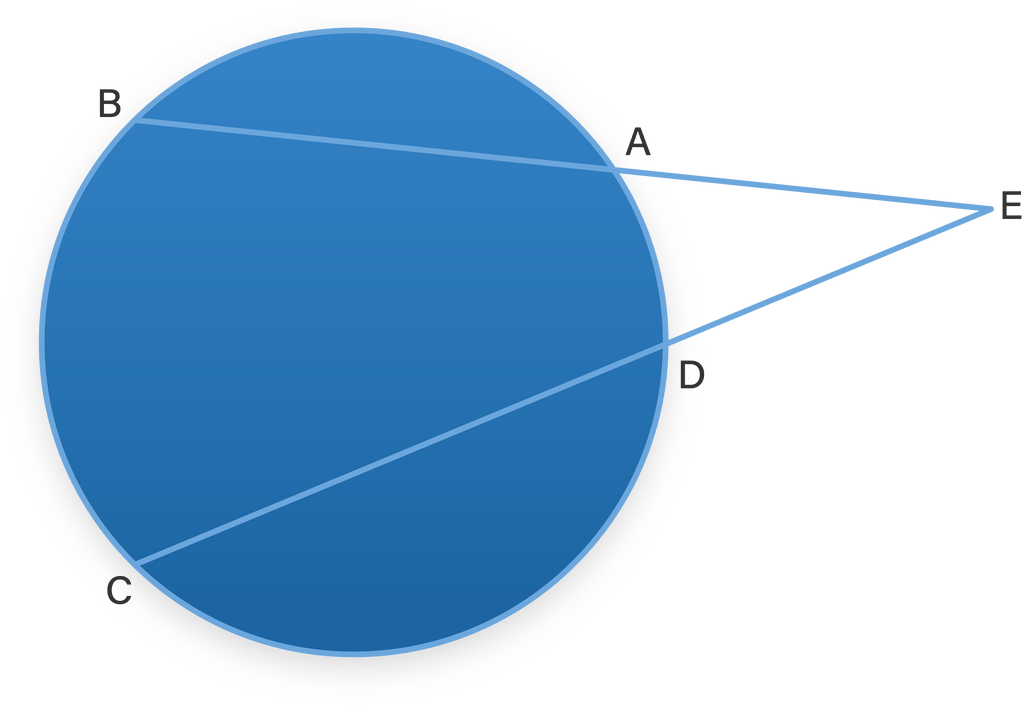
Diketahui lingkaran dengan tali busur A B dan C D berpotongan di E di luar lingkaran. Busur kecil A D berhadapan dengan sudut pusat 4 2 ∘ dan busur kecil BC berhadapan dengan sudut pusat 8 6 ∘ . a. Tentukan besar ∠ A C D . b. Tentukan besar ∠ C A B . c. Gunakan segitiga A EC untuk menghitung besar ∠ A E D . Berikan pendapatmu tentang hasil ini.

Diketahui lingkaran dengan tali busur $A B$ dan $C D$ berpotongan di $E$ di luar lingkaran. Busur kecil $A D$ berhadapan dengan sudut pusat $4 2^{\circ}$ dan busur kecil $BC$ berhadapan dengan sudut pusat $8 6^{\circ}$ .

a. Tentukan besar $∠ A C D$ .

b. Tentukan besar $∠ C A B$ .

c. Gunakan segitiga $A EC$ untuk menghitung besar $∠ A E D$ . Berikan pendapatmu tentang hasil ini.

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

H. Eka

Master Teacher

Mahasiswa/Alumni Universitas Pendidikan Indonesia

Jawaban terverifikasi

Jawaban

diperolehbesar ∠ ACD = 2 1 ∘ , ∠ CAB = 4 3 ∘ , dan ∠ AED = 2 2 ∘ . Besar ∠ AED dapat ditentukan dari setengah kali selisihsudut pusat yang terletak di antara kedua tali busur AB dan CD .

diperoleh besar

∠ ACD = 2 1^{\circ}

∠ CAB = 4 3^{\circ}

, dan

∠ AED = 2 2^{\circ}

. Besar

∠ AED

dapat ditentukan dari setengah kali selisih sudut pusat yang terletak di antara kedua tali busur

AB

dan

CD

Pembahasan

Jawaban yang benar untuk pertanyaan tersebut adalah: a. b. c. .Besar ∠ AED dapat ditentukan dari setengah kali selisihsudut pusat yang terletak di antara kedua tali busur AB dan CD . Jika sudut pusat lingkaran dan sudut keliliing lingkaran menghadap busur yang sama, maka besar sudut pusat adalah dua kalidari besar sudut keliling. Sudutpusat = 2 × Sudutkeliling atau Sudutkeliling = 2 1 × Sudutpusat Jika ada dua tali busur saling berpotongan di luar lingkaran, maka besar sudut antara dua tali busur yang berpotongan di luar lingkaran sama dengan setengah kali selisih sudut pusat yang terletak di antara kedua tali busur tersebut. a. Besar ∠ ACD dapat ditentukan sebagai berikut. Sudut keliling ACD menghadap busur yang sama dengan sudut pusat 4 2 ∘ sehingga diperoleh: ∠ ACD = = 2 1 × 4 2 ∘ 2 1 ∘ Diperoleh besar ∠ ACD = 2 1 ∘ b.Besar ∠ CAB dapat ditentukan sebagai berikut. Sudut keliling CAB menghadap busur yang sama dengan sudut pusat 8 6 ∘ sehingga diperoleh: ∠ CAB = = 2 1 × 8 6 ∘ 4 3 ∘ Diperoleh besar ∠ CAB = 4 3 ∘ . c. Pada segitiga AEC , besar ∠ ACE = ∠ ACD = 2 1 ∘ dan ∠ CAE berpelurus dengan sudut ∠ CAB . Besar ∠ CAE , yaitu: ∠ CAE + ∠ CAB ∠ CAE + 4 3 ∘ ∠ CAE = = = 18 0 ∘ 18 0 ∘ 13 7 ∘ Jumlah sudut dalam segitiga adalah 18 0 ∘ sehingga besar ∠ AED dapat ditentukan sebagai berikut. ∠ ACE + ∠ CAE + ∠ AED 2 1 ∘ + 13 7 ∘ + ∠ AED 15 8 ∘ + ∠ AED ∠ AED = = = = 18 0 ∘ 18 0 ∘ 18 0 ∘ 2 2 ∘ Diperoleh besar ∠ AED = 2 2 ∘ Besar ∠ AED = 2 2 ∘ juga dapat ditentukan sebagai berikut. ∠ AED 2 2 ∘ 2 2 ∘ 2 2 ∘ = = = = 2 1 × ( ∠ BOC − ∠ AOD ) 2 1 × ( 8 6 ∘ − 4 2 ∘ ) 2 1 × 4 4 ∘ 2 2 ∘ Jadi, jika ada dua tali busur saling berpotongan di luar lingkaran, maka besar sudut antara dua tali busur yang berpotongan di luar lingkaran sama dengan setengah kali selisih sudut pusat yang terletak di antara kedua tali busur tersebut. Dengan demikian, diperolehbesar ∠ ACD = 2 1 ∘ , ∠ CAB = 4 3 ∘ , dan ∠ AED = 2 2 ∘ . Besar ∠ AED dapat ditentukan dari setengah kali selisihsudut pusat yang terletak di antara kedua tali busur AB dan CD .

Jawaban yang benar untuk pertanyaan tersebut adalah:

a. $\boldsymbol\angle\textbf{ACD}\boldsymbol=\mathbf{21}\boldsymbol\textdegree$

b. $\boldsymbol\angle\textbf{CAB}\boldsymbol=\mathbf{43}\boldsymbol\textdegree$

c. $\boldsymbol\angle\textbf{AED}\boldsymbol=\mathbf{22}\boldsymbol\textdegree$ . Besar $∠ AED$ dapat ditentukan dari setengah kali selisih sudut pusat yang terletak di antara kedua tali busur $AB$ dan $CD$ .

Jika sudut pusat lingkaran dan sudut keliliing lingkaran menghadap busur yang sama, maka besar sudut pusat adalah dua kali dari besar sudut keliling.

$Sudut pusat = 2 \times Sudut keliling$

atau

$Sudut keliling = \frac{1}{2} \times Sudut pusat$

Jika ada dua tali busur saling berpotongan di luar lingkaran, maka besar sudut antara dua tali busur yang berpotongan di luar lingkaran sama dengan setengah kali selisih sudut pusat yang terletak di antara kedua tali busur tersebut.

a. Besar $∠ ACD$ dapat ditentukan sebagai berikut.

Sudut keliling $ACD$ menghadap busur yang sama dengan sudut pusat $4 2^{\circ}$ sehingga diperoleh:

$∠ ACD = = \frac{1}{2} \times 4 2^{\circ} 2 1^{\circ}$

Diperoleh besar $∠ ACD = 2 1^{\circ}$

b. Besar $∠ CAB$ dapat ditentukan sebagai berikut.

Sudut keliling $CAB$ menghadap busur yang sama dengan sudut pusat $8 6^{\circ}$ sehingga diperoleh:

$∠ CAB = = \frac{1}{2} \times 8 6^{\circ} 4 3^{\circ}$

Diperoleh besar $∠ CAB = 4 3^{\circ}$ .

c. Pada segitiga $AEC$ , besar $∠ ACE = ∠ ACD = 2 1^{\circ}$ dan $∠ CAE$ berpelurus dengan sudut $∠ CAB$ . Besar $∠ CAE$ , yaitu:

$∠ CAE + ∠ CAB ∠ CAE + 4 3^{\circ} ∠ CAE = = = 18 0^{\circ} 18 0^{\circ} 13 7^{\circ}$

Jumlah sudut dalam segitiga adalah $18 0^{\circ}$ sehingga besar $∠ AED$ dapat ditentukan sebagai berikut.

$∠ ACE + ∠ CAE + ∠ AED 2 1^{\circ} + 13 7^{\circ} + ∠ AED 15 8^{\circ} + ∠ AED ∠ AED = = = = 18 0^{\circ} 18 0^{\circ} 18 0^{\circ} 2 2^{\circ}$

Diperoleh besar $∠ AED = 2 2^{\circ}$

Besar $∠ AED = 2 2^{\circ}$ juga dapat ditentukan sebagai berikut.

$∠ AED 2 2^{\circ} 2 2^{\circ} 2 2^{\circ} = = = = \frac{1}{2} \times (∠ BOC - ∠ AOD) \frac{1}{2} \times (8 6^{\circ} - 4 2^{\circ}) \frac{1}{2} \times 4 4^{\circ} 2 2^{\circ}$

Jadi, jika ada dua tali busur saling berpotongan di luar lingkaran, maka besar sudut antara dua tali busur yang berpotongan di luar lingkaran sama dengan setengah kali selisih sudut pusat yang terletak di antara kedua tali busur tersebut.

Dengan demikian, diperoleh besar $∠ ACD = 2 1^{\circ}$ , $∠ CAB = 4 3^{\circ}$ , dan $∠ AED = 2 2^{\circ}$ . Besar $∠ AED$ dapat ditentukan dari setengah kali selisih sudut pusat yang terletak di antara kedua tali busur $AB$ dan $CD$ .

Buka akses jawaban yang telah terverifikasi

Yah, akses pembahasan gratismu habis

atau

Dapatkan jawaban pertanyaanmu di AiRIS. Langsung dijawab oleh bestie pintar

Tanya Sekarang

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

5.0 (3 rating)

Aisyah Filhayati

Ini yang aku cari!

Pertanyaan serupa

Diketahui sudut keliling ∠ B A C dan sudut pusat ∠ BOC = 6 0 ∘ . Kita akan menghitung besar sudut keliling tersebut dengan cara mengerjakan soal-soal berikut. a. Jelaskan mengapa segitiga A OB s...

3.6

Jawaban terverifikasi

Diketahui sudut keliling ∠ B A C dan sudut pusat ∠ BOC = 6 0 ∘ . Kita akan menghitung besar sudut keliling tersebut dengan cara mengerjakan soal-soal berikut. c. Jelaskan mengapa segitiga A OC s...

5.0

Jawaban terverifikasi

Perhatikan gambar di bawah ini! Tentukan besar sudut x , y , dan z !

4.8

Jawaban terverifikasi

3.6

Jawaban terverifikasi

5.0

Jawaban terverifikasi

Tanya ke AiRIS

Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

Chat AiRIS