Iklan
Pertanyaan
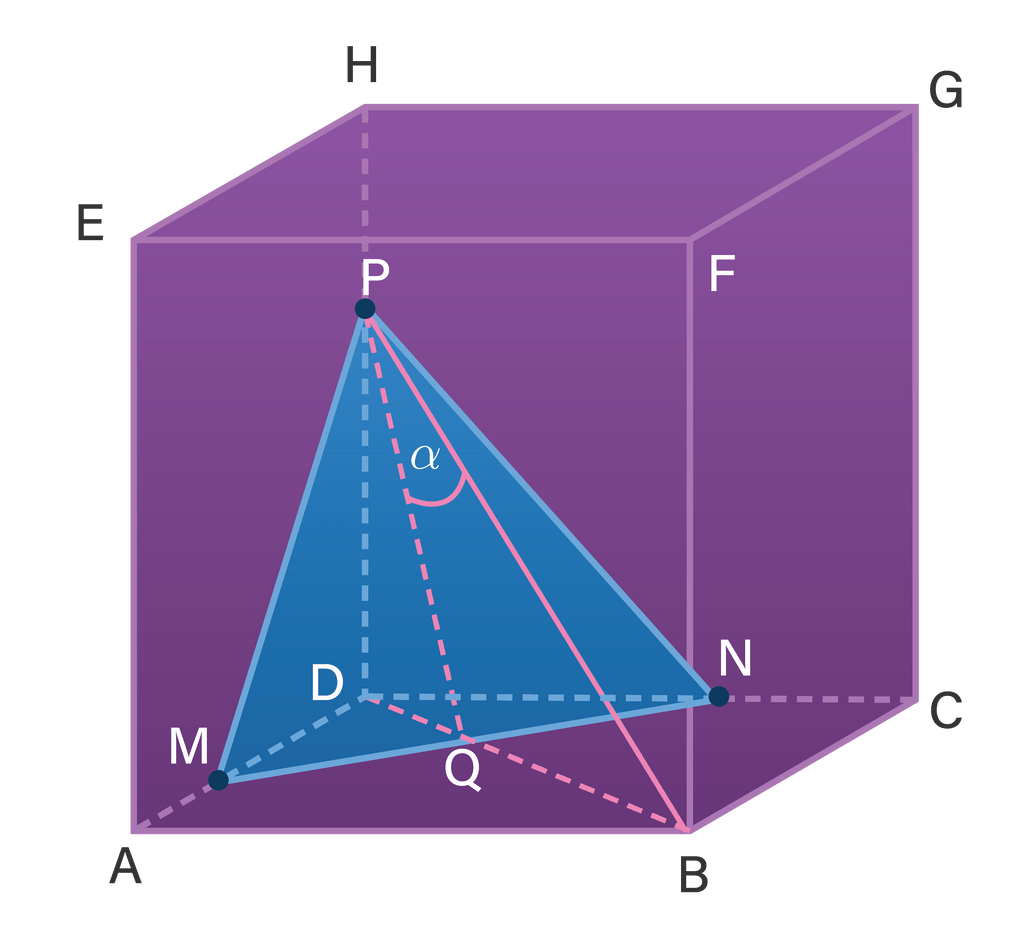
Diketahui kubus ABCD.EFGH . Titik M berada di rusuk AD sedemikian sehingga AM:MD=1:2 , titik N berada di rusuk CD sedemikian sehirigga CN:ND=1:2 . Titik P berada di rusuk DH sedemikian sehingga DP:PH=2:1 . Jika α adalah sudut antara bidang MNP dan garis PB , maka nilai cos α = ...
Diketahui kubus . Titik berada di rusuk sedemikian sehingga , titik berada di rusuk sedemikian sehirigga . Titik berada di rusuk sedemikian sehingga . Jika adalah sudut antara bidang dan garis , maka nilai
Iklan
DF
D. Firmansyah
Master Teacher
Jawaban terverifikasi
2
2.0 (2 rating)
KZ
Keyla Zahira
Jawaban tidak sesuai
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia