Iklan
Pertanyaan
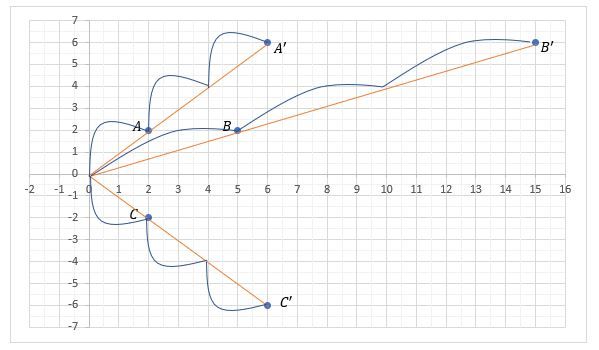
Diketahui ∆ABC dengan titik A ( 2 , 2 ) , B ( 5 , 2 ) , dan C ( 2 , − 2 ) . Oleh dilatasi [ O , 3 ] menghasilkan △ A’B’C’ . a) tentukan koordinat A ′ B ′ C ′ , dengan menggambar dahulu b) tentukan luas △ ABC dan luas △ A’B’C’ c) bagaimana hubungan luas △ ABC dan luas △ A’B’C’
Diketahui dengan titik Oleh dilatasi menghasilkan .
a) tentukan koordinat , dengan menggambar dahulu
b) tentukan luas dan luas
c) bagaimana hubungan luas dan luas
Iklan
DF
D. Firmansyah
Master Teacher
Jawaban terverifikasi
1
5.0 (1 rating)
AD
Alma Dtunggal
Pembahasan lengkap banget
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia