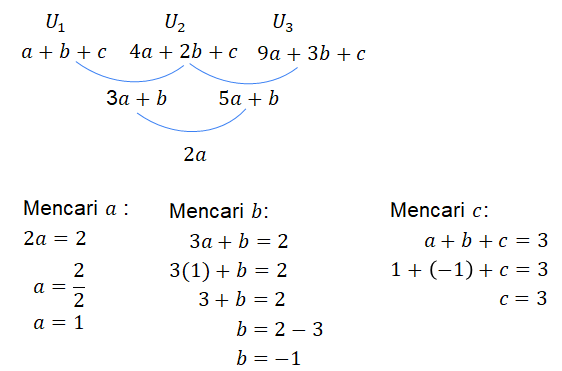Diketahui barisan bilangan 3, 5, 9,15, .... Tentukan: a. rumus suku ke-n;

Pembahasan

Perhatikan pola barisan bilangan! 3, 5, 9,15, .... Beda antara suku pertama dengan suku kedua adalah . Beda antara suku kedua dan suku ketiga adalah . Beda antara suku ketiga dan suku keempat adalah . Hal ini mengakibatkan bahwa kita tidak bisa menggunakan rumus barisan aritmatika biasa. Perhatikan hasil dari selisih suku-suku tersebut! Asumsikan selisih suku-suku itu sebagai barisan baru dan kita cari nilai bedanya, maka diketahui bahwa mereka memiliki nilai beda yang sama atau tetap, yaitu . Jika barisan pertama dianggap sebagai barisan tingkat satu, lalu suku-suku baru yang merupakan hasil selisih barisan dianggap sebagai barisan tingkat dua, maka artinya barisan tersebut termasuk kedalam barisan tingkat duakarena nilai beda tetap dari barisan aritmatika tersebut baru bisa ditemukan di tingkat kedua. 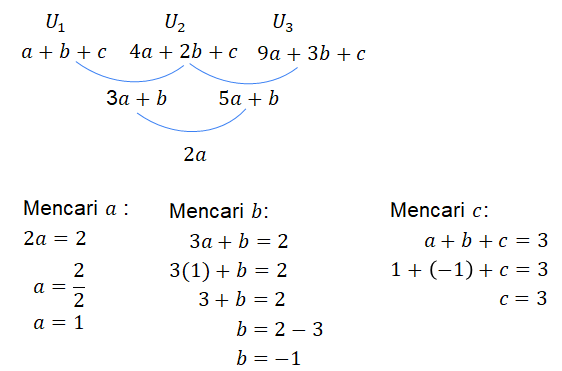Untuk mencari suku ke-n barisan aritmatika tingkat dua, menggunakan rumus : sehingga terbentuk suku ke-n barisan aritmetika sebagai berikut : Dengan demukian rumus suku ke-n barisan aritmetika tersebut adalah