Pertanyaan

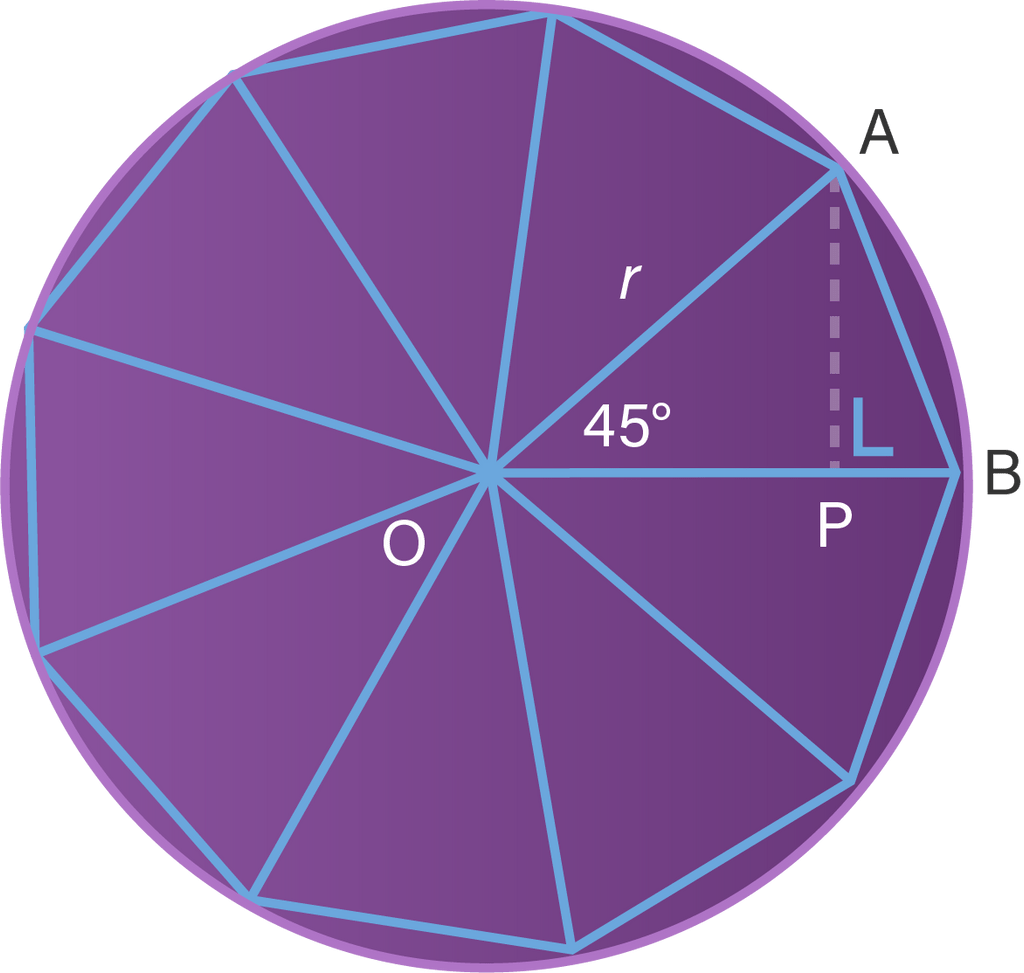
Di dalam lingkaran, dibuat segi- n beraturan, yaitu segi- n dengan panjang sisi sama panjang. Tentukan keliling dan luas segi- n tersebut, dengan terlebih dahulu menghitung besar sudut pusat di hadapan sisi segi- n tersebut, jika: d. n = 8

Di dalam lingkaran, dibuat segi- $n$ beraturan, yaitu segi- $n$ dengan panjang sisi sama panjang. Tentukan keliling dan luas segi- $n$ tersebut, dengan terlebih dahulu menghitung besar sudut pusat di hadapan sisi segi- $n$ tersebut, jika:

d. $n = 8$

HE

H. Eka

Master Teacher

Mahasiswa/Alumni Universitas Pendidikan Indonesia

Jawaban terverifikasi

Jawaban

keliling dan luas delapan beraturantersebut adalah K = 8 r 2 − 2 satuan panjang dan L = 2 r 2 2 satuan luas.

keliling dan luas delapan beraturan tersebut adalah

K = 8 r 2 - 2

satuan panjang dan

L = 2 r^{2} 2

satuan luas.

Pembahasan

Jawaban yang benar untuk pertanyaan tersebut adalah K = 8 r 2 − 2 satuan panjang dan L = 2 r 2 2 satuan luas. Tali busur adalah garis yang menghubungkan dua titik pada lingkaran. Ingat! Teorema Pythagoras: c 2 = a 2 + b 2 dengan panjang sisi miring dan a , b panjang sisi lainnya. Pada segitiga siku-siku, perbandingan panjang sisi di depan sudut 4 5 ∘ , 4 5 ∘ , dan 9 0 ∘ berturut-turutadalah 1 : 1 : 2 . Untuk n = 8 , besar sudut pusat dihadapan segi delapanberaturantersebut, yaitu: 8 36 0 ∘ = 4 5 ∘ Perhatikan gambar segi delapan beraturanberikut. Segi delapanberaturan tersebut terdiri dari delapanbuah segitiga sama kaki. Panjang tali busur atau sisi segi enam beraturantersebut dapat ditentukan sebagai berikut. Panjang OP = AP , yaitu: OA OP r OP OP = = = 2 1 2 1 2 2 r 2 Panjang OP = AP = 2 r 2 sehingga panjang tali busur AB dapat ditentukan sebagai berikut. AB = = = = = = AP 2 + PB 2 ( 2 r 2 ) 2 + ( r − 2 r 2 ) 2 2 r 2 + r 2 − r 2 2 + 2 r 2 2 r 2 − r 2 2 r 2 ( 2 − 2 ) r 2 − 2 Diperoleh panjang sisi segi delapan beraturan, yaitu s = r 2 − 2 satuan panjang. Keliling segi delapan beraturantersebut adalah sebagai berikut. K = = = 8 × s 8 × r 2 − 2 8 r 2 − 2 Luas segi delapanberaturan tersebut dapat ditentukan sebagai berikut. Luassegitiga OAB , yaitu: L △ = = = 2 1 × a × t 2 1 × r × 2 r 2 4 r 2 2 Luas segi delapanberaturan tersebut, yaitu: L = = = 8 × L △ 8 × 4 r 2 2 2 r 2 2 Dengan demikian, keliling dan luas delapan beraturantersebut adalah K = 8 r 2 − 2 satuan panjang dan L = 2 r 2 2 satuan luas.

Jawaban yang benar untuk pertanyaan tersebut adalah $K = 8 r 2 - 2$ satuan panjang dan $L = 2 r^{2} 2$ satuan luas.

Tali busur adalah garis yang menghubungkan dua titik pada lingkaran.

Ingat! Teorema Pythagoras:

$c^{2} = a^{2} + b^{2}$

dengan $c$ panjang sisi miring dan $a, b$ panjang sisi lainnya.

Pada segitiga siku-siku, perbandingan panjang sisi di depan sudut $4 5^{\circ}$ , $4 5^{\circ}$ , dan $9 0^{\circ}$ berturut-turut adalah $1 : 1 : 2$ .

Untuk $n = 8$ , besar sudut pusat dihadapan segi delapan beraturan tersebut, yaitu:

$\frac{36 0 ^{\circ}}{8} = 4 5^{\circ}$

Perhatikan gambar segi delapan beraturan berikut.

Segi delapan beraturan tersebut terdiri dari delapan buah segitiga sama kaki. Panjang tali busur atau sisi segi enam beraturan tersebut dapat ditentukan sebagai berikut.

Panjang $OP = AP$ , yaitu:

$\frac{OP}{OA} \frac{OP}{r} OP = = = \frac{1}{2} \frac{1}{2} 2 \frac{r}{2} 2$

Panjang $OP = AP = \frac{r}{2} 2$ sehingga panjang tali busur $AB$ dapat ditentukan sebagai berikut.

$AB = = = = = = AP^{2} + PB^{2} (\frac{r}{2} 2)^{2} + (r - \frac{r}{2} 2)^{2} \frac{r ^{2}}{2} + r^{2} - r^{2} 2 + \frac{r ^{2}}{2} 2 r^{2} - r^{2} 2 r^{2} (2 - 2) r 2 - 2$

Diperoleh panjang sisi segi delapan beraturan, yaitu $s = r 2 - 2$ satuan panjang.

Keliling segi delapan beraturan tersebut adalah sebagai berikut.

$K = = = 8 \times s 8 \times r 2 - 2 8 r 2 - 2$

Luas segi delapan beraturan tersebut dapat ditentukan sebagai berikut.

Luas segitiga $OAB$ , yaitu:

$L_{△} = = = \frac{1}{2} \times a \times t \frac{1}{2} \times r \times \frac{r}{2} 2 \frac{r ^{2}}{4} 2$

Luas segi delapan beraturan tersebut, yaitu:

$L = = = 8 \times L_{△} 8 \times \frac{r ^{2}}{4} 2 2 r^{2} 2$

Dengan demikian, keliling dan luas delapan beraturan tersebut adalah $K = 8 r 2 - 2$ satuan panjang dan $L = 2 r^{2} 2$ satuan luas.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

2

2.0 (1 rating)

LA

Latifah Angraini Siregar

Jawaban tidak sesuai