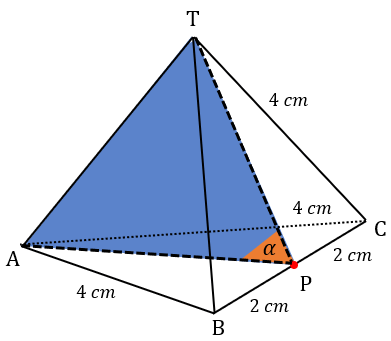
Bidang empat beraturan T.ABCmemiliki panjang rusuk 4 cm . Diketahui titik P terletak pada pertengahan rusuk BC. Nilai tangen sudut antara ruas garis TP dengan bidang alas adalah ....

Pembahasan

Perhatikan gambar di bawah ini! Karena T.ABC adalah bidang empat beraturan, proyeksi titik T pada bidang alas akan terletak pada ruas garis AP. Dengan demikian, sudut antara TP dan bidang alas diwakili oleh sudut TPA yang diwakili dengan sudut . Dengan demikian, pada soal ini akan dicari nilai dari . Perhatikan bahwa seluruh segitiga yang menyusun bidang empat beraturan T.ABC adalah segitiga sama sisi dengan panjang rusuk . Karena segitiga ABC dan TBC sama sisi dan titik P terletak di pertengahan BC, maka panjang . Pada segitiga ABC, ruas garis AP merupakan garis berat. Karena segitiga ABC sama sisi, maka ruas garis AP juga merupakan garis tinggi. Dengan menggunakan Teorema Pythagoras pada segitiga ABP, diperoleh perhitungan sebagai berikut. Karena panjang ruas garis AP tidak mungkin negatif, maka cm. Kemudian, dengan menggunakan aturan cosinus, didapat perhitungan sebagai berikut. Selanjutnya, dengan menggunakan identitas trigonometri, didapat hasil sebagai berikut. Pada gambar di atas, dapat diperhatikan bahwa sudut yang terbentuk adalah sudut lancip sehingga bernilai positif. Dengan demikian, . Jadi, jawaban yang tepatadalah C.