Pertanyaan

Arsirlah himpunan penyelesaian dari masing-masing sistem pertidaksamaan berikut pada sistem koordinat Cartesius. y ≤ x 2 − 5 x − 6 ; x ≥ 0 dan x + 2 y ≤ 4

Arsirlah himpunan penyelesaian dari masing-masing sistem pertidaksamaan berikut pada sistem koordinat Cartesius.

$y \leq x^{2} - 5 x - 6; x \geq 0 dan x + 2 y \leq 4$

N. Puspita

Master Teacher

Jawaban terverifikasi

Pembahasan

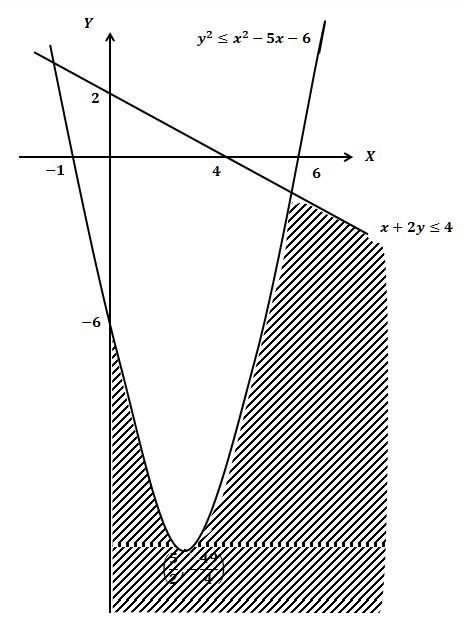
Untuk mencari penyelesaian dari sistem pertidaksamaan y ≤ x 2 − 5 x − 6 ; x ≥ 0 dan x + 2 y ≤ 4 pada sistem koordinat Cartesius, berikut ini langkah-langkahnya: Gambar grafik y ≤ x 2 − 5 x − 6 Grafik y = x 2 − 5 x − 6 adalah kurva berbentuk parabola dengan titik potong terhadap sumbu X jika y = 0 sehingga y 0 0 x = = = = x 2 − 5 x − 6 x 2 − 5 x − 6 ( x − 6 ) ( x + 1 ) 6 dan x = − 1 Jadi, parabola y = x 2 − 5 x − 6 berpotongan dengan sumbu X di titik ( − 1 , 0 ) dan ( 6 , 0 ) . Selanjutnya,titik potong terhadap sumbu Y jika x = 0 sehingga y = x 2 − 5 x − 6 = 0 2 − 5 ⋅ 0 − 6 = − 6 .Jadi, parabola y = x 2 − 5 x − 6 berpotongan dengan sumbu Y di titik ( 0 , − 6 ) . Mencari titik puncak parabola y = x 2 − 5 x − 6 yaitu: x y = = = = 2 a − b = 2 ⋅ 1 − ( − 5 ) = 2 5 4 a − D = 4 a − ( b 2 − 4 a c ) 4 ⋅ 1 − ( ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) ) 4 − ( 25 + 24 ) = 4 − 49 Jadi, titik puncak parabola y = x 2 − 5 x − 6 adalah ( 2 5 , 4 − 49 ) . Gambar grafik x + 2 y ≤ 4 Grafik x + 2 y = 4 adalah garis dengan titik potong terhadap sumbu X jika y = 0 sehingga x + 2 y x + 2 ⋅ 0 x + 0 x = = = = 4 4 4 4 . Jadi, garis x + 2 y = 4 berpotongan dengan sumbu X di titik ( 4 , 0 ) . Selanjutnya,titik potong terhadap sumbu Y jika x = 0 sehingga x + 2 y 0 + 2 y 2 y y = = = = 4 4 4 2 4 = 2 Jadi, garis x + 2 y = 4 berpotongan dengan sumbu Y di titik ( 0 , 2 ) . Di bawah ini adalah hasil gambarpenyelesaian dari sistem pertidaksamaan y ≤ x 2 − 5 x − 6 ; x ≥ 0 dan x + 2 y ≤ 4 Uji titik ( 0 , 0 ) pada y ≤ x 2 − 5 x − 6 . Jelas bahwa y y y ≤ ≤ ≤ x 2 − 5 x − 6 0 2 − 5 ⋅ 0 − 6 − 6 sedangkan 0 > − 6 Artinya,titik ( 0 , 0 ) tidak terletak pada daerah penyelesaian y ≤ x 2 − 5 x − 6 . Uji titik ( 0 , 0 ) pada x + 2 y ≤ 4 . Jelas bahwa x + 2 y 0 + 2 ⋅ 0 0 ≤ ≤ ≤ 4 4 4 Artinya,titik ( 0 , 0 ) terletak pada daerah penyelesaian x + 2 y ≤ 4 . Jadi, gambar himpunan penyelesaian darisistem pertidaksamaan y ≤ x 2 − 5 x − 6 ; x ≥ 0 dan x + 2 y ≤ 4 adalah

Untuk mencari penyelesaian dari sistem pertidaksamaan $y \leq x^{2} - 5 x - 6; x \geq 0 dan x + 2 y \leq 4$ pada sistem koordinat Cartesius, berikut ini langkah-langkahnya:

Gambar grafik $y \leq x^{2} - 5 x - 6$

Grafik $y = x^{2} - 5 x - 6$ adalah kurva berbentuk parabola dengan titik potong terhadap sumbu $X$ jika $y = 0$ sehingga

$y 00 x = = = = x^{2} - 5 x - 6 x^{2} - 5 x - 6 (x - 6) (x + 1) 6 dan x = - 1$

Jadi, parabola $y = x^{2} - 5 x - 6$ berpotongan dengan sumbu $X$ di titik $(- 1, 0)$ dan $(6, 0)$ .

Selanjutnya, titik potong terhadap sumbu $Y$ jika $x = 0$ sehingga $y = x^{2} - 5 x - 6 = 0^{2} - 5 \cdot 0 - 6 = - 6$ .Jadi, parabola $y = x^{2} - 5 x - 6$ berpotongan dengan sumbu $Y$ di titik $(0, - 6)$ .

Mencari titik puncak parabola $y = x^{2} - 5 x - 6$ yaitu:

$x y = = = = \frac{- b}{2 a} = \frac{- ( - 5 )}{2 \cdot 1} = \frac{5}{2} \frac{- D}{4 a} = \frac{- ( b ^{2} - 4 a c )}{4 a} \frac{- ( ( - 5 ) ^{2} - 4 \cdot 1 \cdot ( - 6 ) )}{4 \cdot 1} \frac{- ( 25 + 24 )}{4} = \frac{- 49}{4}$