Iklan
Pertanyaan
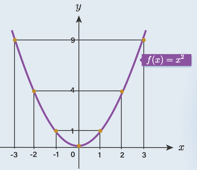
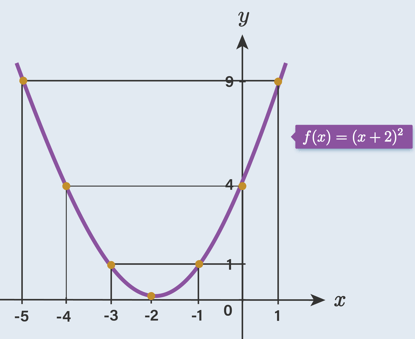
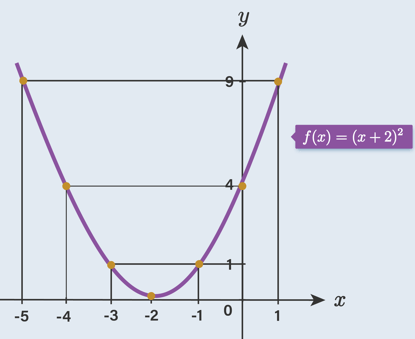
3 a. Cobalah kalian bandingkan bentuk grafik fungsi f ( x ) = ( x + 2 ) 2 dan f ( x ) = ( x − 3 ) 2 !Apakah kedua grafik tersebut memiliki bentuk yang sama? 3 b. Selanjutnya, bandingkanlah bentuk grafik fungsi f ( x ) = ( x + 2 ) 2 dan f ( x ) = ( x − 3 ) 2 terhadap grafik fungsi f ( x ) = x 2 ! Bagaimana bentuk ketiga grafik tersebut? 3 c. Kesimpulan apa yang dapat diambil untuk ketiga grafik di atas? 4.Grafik fungsi f ( x ) = ( x + 2 ) 2 memiliki titik balik minimum ( ... , ... ) dan grafik fungsi f ( x ) = ( x − 3 ) 2 memiliki titik balik minimum ( ... , ... ) . Berapakah koordinat titik balik minimum dari fungsi f ( x ) = ( x + p ) 2 dan f ( x ) = ( x − q ) 2 ?
3 a. Cobalah kalian bandingkan bentuk grafik fungsi dan ! Apakah kedua grafik tersebut memiliki bentuk yang sama?
3 b. Selanjutnya, bandingkanlah bentuk grafik fungsi dan terhadap grafik fungsi ! Bagaimana bentuk ketiga grafik tersebut?
3 c. Kesimpulan apa yang dapat diambil untuk ketiga grafik di atas?
4. Grafik fungsi memiliki titik balik minimum dan grafik fungsi memiliki titik balik minimum . Berapakah koordinat titik balik minimum dari fungsi dan ?
Iklan
L. Rante
Master Teacher
Mahasiswa/Alumni Universitas Negeri Makassar
2
4.6 (5 rating)
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia