Riesya A
08 Februari 2024 09:21
Iklan
Riesya A
08 Februari 2024 09:21
Pertanyaan
Fungsi f(x) = 4 sin x + 4 cos x yang didefinisikan pada interval 0 ≤ x ≤ 2π mencapai nilai maksimum untuk titik x = .... A. π/6 B. π/4 C. π/3 D. π/2 E. 3π/4
Fungsi f(x) = 4 sin x + 4 cos x yang didefinisikan pada interval 0 ≤ x ≤ 2π mencapai nilai maksimum untuk titik x = ....
A. π/6
B. π/4
C. π/3
D. π/2
E. 3π/4
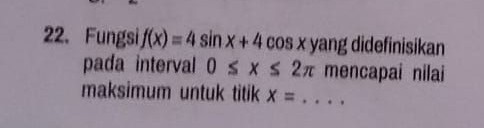
87
2
Iklan
Tjendana T

Community
08 Februari 2024 14:49
<p>Jawaban <strong>B. π/4</strong></p><p> </p><p><strong>Pembahasan </strong></p><p>f(x) = 4 sin x + 4 cos x</p><p> </p><p>Mencari fungsi max. dgn turunan pertama dari fungsi tsb.</p><p> </p><p>f'(x) = 0</p><p><=> 4 cos x - 4 sin x = 0</p><p><=> 4 cos x = 4 sin x</p><p><=> cos x = sin x</p><p>Nilai x yg memenuhi adalah 45° atau π/4</p><p> </p><p> </p>
Jawaban B. π/4
Pembahasan
f(x) = 4 sin x + 4 cos x
Mencari fungsi max. dgn turunan pertama dari fungsi tsb.
f'(x) = 0
<=> 4 cos x - 4 sin x = 0
<=> 4 cos x = 4 sin x
<=> cos x = sin x
Nilai x yg memenuhi adalah 45° atau π/4
· 5.0 (2)
Iklan
ADAM M
31 Maret 2024 18:35
<p>Baik, mari kita menggunakan not</p><p>1. Hitung turunan pertama dari fungsi \( f(x) = 4 \sin x + 4 \cos x \):<br>\[ f'(x) = 4 \cos x - 4 \sin x \]</p><p>2. Setel turunan pertama sama dengan nol dan cari nilai \( x \):<br>\[ 4 \cos x - 4 \sin x = 0 \]</p><p>3. Dari persamaan tersebut, kita dapat menyederhanakannya menjadi \( \cos x = \sin x \).</p><p>4. Titik-titik di mana \( \cos x = \sin x \) adalah \( x = \frac{\pi}{4} + 2n\pi \), di mana \( n \) adalah bilangan bulat.</p><p>5. Karena interval yang diberikan adalah \( 0 \leq x \leq 2 \), kita perlu memeriksa apakah nilai \( x = \frac{\pi}{4} \) berada dalam interval tersebut. Karena \( 0 \leq \frac{\pi}{4} \leq 2 \), maka \( x = \frac{\pi}{4} \) merupakan kandidat nilai maksimum.</p><p>Jadi, nilai maksimum dari fungsi \( f(x) \) terjadi saat \( x = \frac{\pi}{4} \).</p>
Baik, mari kita menggunakan not
1. Hitung turunan pertama dari fungsi \( f(x) = 4 \sin x + 4 \cos x \):
\[ f'(x) = 4 \cos x - 4 \sin x \]
2. Setel turunan pertama sama dengan nol dan cari nilai \( x \):
\[ 4 \cos x - 4 \sin x = 0 \]
3. Dari persamaan tersebut, kita dapat menyederhanakannya menjadi \( \cos x = \sin x \).
4. Titik-titik di mana \( \cos x = \sin x \) adalah \( x = \frac{\pi}{4} + 2n\pi \), di mana \( n \) adalah bilangan bulat.
5. Karena interval yang diberikan adalah \( 0 \leq x \leq 2 \), kita perlu memeriksa apakah nilai \( x = \frac{\pi}{4} \) berada dalam interval tersebut. Karena \( 0 \leq \frac{\pi}{4} \leq 2 \), maka \( x = \frac{\pi}{4} \) merupakan kandidat nilai maksimum.
Jadi, nilai maksimum dari fungsi \( f(x) \) terjadi saat \( x = \frac{\pi}{4} \).
· 0.0 (0)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



