Pradnyani P
20 Maret 2025 14:01
Iklan
Pradnyani P
20 Maret 2025 14:01
Pertanyaan
Tentukan batas-batas nilai m agar fungsi kuadrat f(x) = (m - 1)x² + (m + 7)x + (2m-1) memotong sumbu X di dua titik yang berbeda! Tolong dijawab dengan pembahasan yang lengkap yaaa Terima kasih♡
Tentukan batas-batas nilai m agar fungsi kuadrat f(x) = (m - 1)x² + (m + 7)x + (2m-1) memotong sumbu X di dua titik yang berbeda!
Tolong dijawab dengan pembahasan yang lengkap yaaa
Terima kasih♡
2
3
Iklan
E. Nur
21 Maret 2025 04:00
Pembahasan pada gambar terlampir
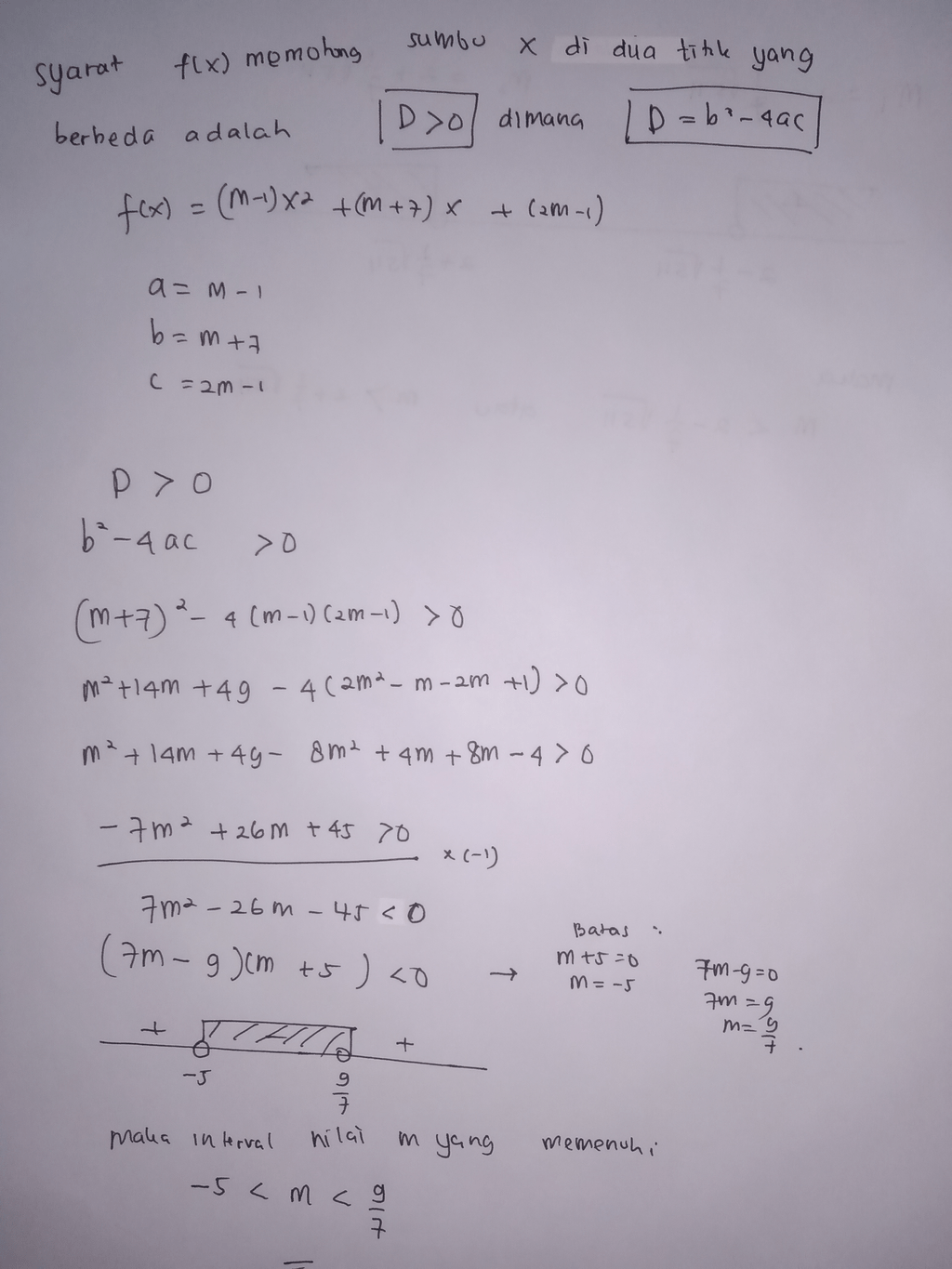
· 5.0 (3)
FITRI D
24 Maret 2025 17:53
BELI ILMU NYA!!!Rp.450.000.000.00,-!!!OKE.
Iklan
Yosua Y
21 Maret 2025 03:00
<p>Ketika terdapat fungsi</p><p>f(x) = ax<sup>2</sup> + bx + c</p><p>Kita bisa menentukan nilai x yang memotong sumbu X (yakni ketika f(x) = 0) sebagai berikut:<br>ax<sup>2</sup> + bx + c = 0</p><p>x<sup>2</sup> + (b/a)x + c/a = 0<br>Perhatikan bahwa:<br>(x + (b/2a))(x + (b/2a)) = x<sup>2</sup> + (b/a)x + b<sup>2</sup>/4a<sup>2</sup></p><p>(x + (b/2a))<sup>2</sup> = x<sup>2</sup> + (b/a)x + b<sup>2</sup>/4a<sup>2</sup></p><p>Dengan demikian x<sup>2</sup> + (b/a)x + c/a = 0 dapat ditulis kembali menjadi:</p><p>(x + (b/2a))<sup>2</sup> - b<sup>2</sup>/4a<sup>2 </sup>+ c/a = 0</p><p>(x + (b/2a))<sup>2</sup> - b<sup>2</sup>/4a<sup>2 </sup>+ 4ac/4a<sup>2</sup> = 0</p><p>(x + (b/2a))<sup>2 </sup>= b<sup>2</sup>/4a<sup>2 </sup>-4ac/4a<sup>2</sup></p><p>(x + (b/2a))<sup>2</sup> = (b<sup>2</sup>-4ac)/4a<sup>2</sup></p><p>(x + (b/2a)) = ±√(b<sup>2</sup>-4ac)/2a</p><p>x = (-b±√(b<sup>2</sup>-4ac))/2a</p><p> </p><p>Agar x memotong di dua titik, nilai dari b<sup>2</sup>-4ac atau yang umumnya dikenal sebagai diskriminan (D) harus lebih besar dari 0 (D>0). Kenapa tidak boleh 0? Karena jika D = 0, maka f(x) akan memotong sumbu X di satu titik saja (ditandai dengan hanya ada 1 penyelesaian nilai x). Jika D<0, nilai x bukanlah bilangan riil. Dengan demikian, ditentukan nilai m sebagai berikut:<br><br>D > 0</p><p>b<sup>2</sup>-4ac > 0</p><p>(m + 7)<sup>2</sup> - 4(m-1)(2m-1) > 0</p><p>m<sup>2</sup> + 14m + 49 - 4(2m<sup>2</sup>-3m+1) > 0</p><p>m<sup>2</sup> + 14m + 49 - 8m<sup>2</sup> + 12m - 4 > 0</p><p>-7m<sup>2</sup> + 26m + 45 > 0</p><p>7m<sup>2</sup> - 26m - 45 < 0</p><p>(7m-9)(m + 5) < 0<br>-5 < m < 9/7</p><p> </p><p>Dengan demikian, jawabannya adalah -5 < m < 9/7.</p><p> </p>
Ketika terdapat fungsi
f(x) = ax2 + bx + c
Kita bisa menentukan nilai x yang memotong sumbu X (yakni ketika f(x) = 0) sebagai berikut:
ax2 + bx + c = 0
x2 + (b/a)x + c/a = 0
Perhatikan bahwa:
(x + (b/2a))(x + (b/2a)) = x2 + (b/a)x + b2/4a2
(x + (b/2a))2 = x2 + (b/a)x + b2/4a2
Dengan demikian x2 + (b/a)x + c/a = 0 dapat ditulis kembali menjadi:
(x + (b/2a))2 - b2/4a2 + c/a = 0
(x + (b/2a))2 - b2/4a2 + 4ac/4a2 = 0
(x + (b/2a))2 = b2/4a2 -4ac/4a2
(x + (b/2a))2 = (b2-4ac)/4a2
(x + (b/2a)) = ±√(b2-4ac)/2a
x = (-b±√(b2-4ac))/2a
Agar x memotong di dua titik, nilai dari b2-4ac atau yang umumnya dikenal sebagai diskriminan (D) harus lebih besar dari 0 (D>0). Kenapa tidak boleh 0? Karena jika D = 0, maka f(x) akan memotong sumbu X di satu titik saja (ditandai dengan hanya ada 1 penyelesaian nilai x). Jika D<0, nilai x bukanlah bilangan riil. Dengan demikian, ditentukan nilai m sebagai berikut:
D > 0
b2-4ac > 0
(m + 7)2 - 4(m-1)(2m-1) > 0
m2 + 14m + 49 - 4(2m2-3m+1) > 0
m2 + 14m + 49 - 8m2 + 12m - 4 > 0
-7m2 + 26m + 45 > 0
7m2 - 26m - 45 < 0
(7m-9)(m + 5) < 0
-5 < m < 9/7
Dengan demikian, jawabannya adalah -5 < m < 9/7.
· 4.7 (3)
RAISSA A
21 Maret 2025 13:24
<p>Inequality:<br>7m² - 26m - 45 < 0<br>Karena koefisien m² positif, maka daerah solusi berada di antara akar-akarnya:</p><p>-9/7 < m < 5</p><p>Agar fungsi memotong sumbu X di dua titik sehingga berbeda, nilai m harus memenuhi:</p><p>-9/7 < m < 5</p>
Inequality:
7m² - 26m - 45 < 0
Karena koefisien m² positif, maka daerah solusi berada di antara akar-akarnya:
-9/7 < m < 5
Agar fungsi memotong sumbu X di dua titik sehingga berbeda, nilai m harus memenuhi:
-9/7 < m < 5
· 5.0 (1)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



