Pertanyaan

Contoh Soal $4.3$ berisi: Tiap papan berputar pada Gambar $4.4$ diputar satu kali. Ambil $X_1$ menyatakan angka yang diperoleh dari papan $A$ , dan $X_2$ menyatakan angka yang diperoleh dari papan $B$ . Tunjukkan bahwa $Y=X_1+X_2$ adalah variabel acak diskrit.

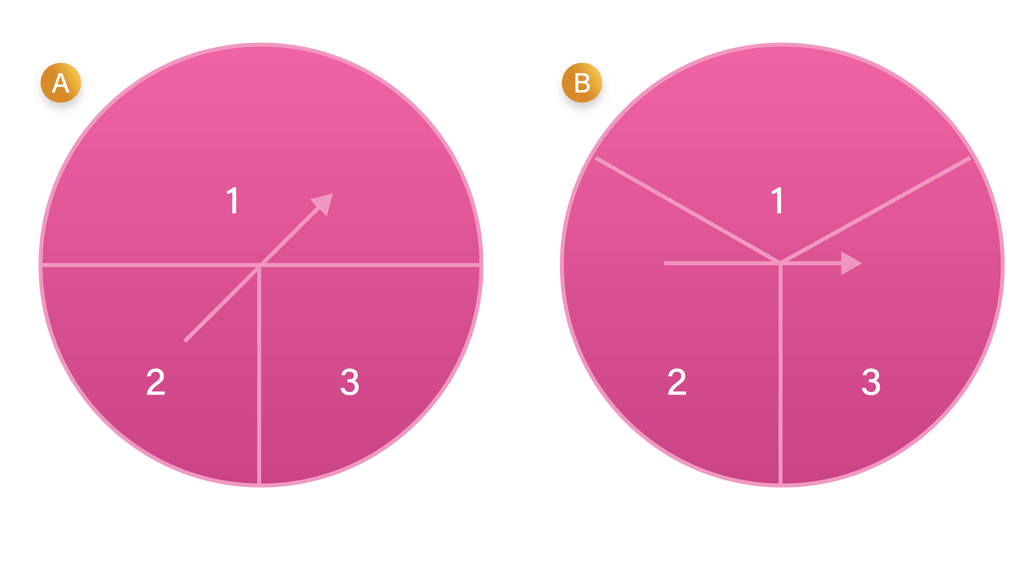
Gambar $4.4$

Untuk masalah seperti dalam Contoh Soal 4.3 , periksalah apakah Y = X 2 − X 1 merupakan suatu variabel acak diskrit? Jelaskan.

Untuk masalah seperti dalam Contoh Soal $4.3$ , periksalah apakah $Y = X_{2} - X_{1}$ merupakan suatu variabel acak diskrit? Jelaskan.

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

T. Prita

Master Teacher

Mahasiswa/Alumni Universitas Negeri Jember

Jawaban terverifikasi

Jawaban

Y = X 2 − X 1 bukan suatu variabel acak diskrit.

Y = X_{2} - X_{1}

bukan suatu variabel acak diskrit.

Pembahasan

Jawaban yang benar dari pertanyaan tersebut telah ditunjukkan bahwa Y = X 2 − X 1 bukan suatu variabel acak diskrit. Konsep peluang: P ( K ) = n ( S ) n ( K ) Keterangan: P ( K ) : peluang kejadian K , dengan 0 ≤ P ( K ) ≤ 1 n ( K ) : banyak anggota dalam kejadian K n ( S ) : banyak anggota dalam himpunan ruang sampel Fungsi f ( x ) merupakan suatu fungsi peluang suatu peubah acak diskrit X dengan syarat: 1. f ( x ) ≥ 0 2. x ∑ f ( x ) = 1 , dengan P ( X = x ) = f ( x ) Penyelesaian soal di atas sebagai berikut. 1. Peluang muncul angka 2 dan angka 3 pada papan A adalah P ( A 2 ) = P ( A 3 ) = 4 1 . Sedangkan peluang muncul angka 1 pada papan A adalah P ( A 1 ) = 4 2 = 2 1 . Perhatikan pada papan A , luas sektor 2 = luas sektor 3 = 2 1 × luas sektor 1 . 2. Pada papan B , luas ketiga sektor adalah sama, sehingga P ( B 1 ) = P ( B 2 ) = P ( B 3 ) = 3 1 . 3. Untuk Y = X 1 − X 2 dimana X 1 menyatakan angka yang diperoleh dari papan A dan X 2 menyatakan angka yang diperoleh dari papan B , diperoleh hasil-hasil probabilitasnya pada tabel berikut. Berdasarkan tabel di atas diperoleh: = = = P ( Y = 0 ∪ Y = 1 ∪ Y = 2 ) P ( Y = 0 ) + P ( Y = 1 ) + P ( Y = 2 ) 12 4 + 12 3 + 12 2 12 9 Syarat f ( x ) ≥ 0 terpenuhi namun syarat x ∑ f ( x ) = 1 , dengan P ( X = x ) = f ( x ) tidak terpenuhi. Dengan demikian Y = X 2 − X 1 bukan suatu variabel acak diskrit.

Jawaban yang benar dari pertanyaan tersebut telah ditunjukkan bahwa $Y = X_{2} - X_{1}$ bukan suatu variabel acak diskrit.

Konsep peluang:

$P (K) = \frac{n ( K )}{n ( S )}$

Keterangan:
$P (K) : peluang kejadian K, dengan 0 \leq P (K) \leq 1 n (K) : banyak anggota dalam kejadian K n (S) : banyak anggota dalam himpunan ruang sampel$

Fungsi $f (x)$ merupakan suatu fungsi peluang suatu peubah acak diskrit $X$ dengan syarat:
1. $f (x) \geq 0$
2. $x \sum f (x) = 1, dengan P (X = x) = f (x)$

Penyelesaian soal di atas sebagai berikut.

1. Peluang muncul angka $2$ dan angka $3$ pada papan $A$ adalah $P (A 2) = P (A 3) = \frac{1}{4}$ .
Sedangkan peluang muncul angka $1$ pada papan $A$ adalah $P (A 1) = \frac{2}{4} = \frac{1}{2}$ .
Perhatikan pada papan $A$ , $luas sektor 2 = luas sektor 3 = \frac{1}{2} \times luas sektor 1$ .

2. Pada papan $B$ , luas ketiga sektor adalah sama, sehingga $P (B 1) = P (B 2) = P (B 3) = \frac{1}{3}$ .

3. Untuk $Y = X_{1} - X_{2}$ dimana $X_{1}$ menyatakan angka yang diperoleh dari papan $A$ dan $X_{2}$ menyatakan angka yang diperoleh dari papan $B$ , diperoleh hasil-hasil probabilitasnya pada tabel berikut.

Berdasarkan tabel di atas diperoleh:

$= = = P (Y = 0 \cup Y = 1 \cup Y = 2) P (Y = 0) + P (Y = 1) + P (Y = 2) \frac{4}{12} + \frac{3}{12} + \frac{2}{12} \frac{9}{12}$

Syarat $f (x) \geq 0$ terpenuhi namun syarat $x \sum f (x) = 1, dengan P (X = x) = f (x)$ tidak terpenuhi.

Dengan demikian $Y = X_{2} - X_{1}$ bukan suatu variabel acak diskrit.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.4 (7 rating)

Nggaktau

Ini yang aku cari!

Digital cell

Respon terlalu lambat

Pertanyaan serupa

Diketahui variabel acak dengan fungsi peluang f ( x ) = k ( 2 1 ) x untuk x = 1 , 2 , 3 dan bernilai 0 untuk x yang lain. Nilai k yang memenuhi adalah ....

4.7

Jawaban terverifikasi

Tabel distribusi peluang variabel acak X berikut Nilai P ( 3 < x ≤ 5 ) = ...

331

4.6

Jawaban terverifikasi

Suatu variabel acak X memiliki distribusi probabilitas seperti pada tabel berikut: dengan k adalah suatu konstanta. Nilai k adalah ....

5.0

Jawaban terverifikasi

Tabel distribusi kumulatif variabel acak X berikut Nilai P ( 3 < X ≤ 5 ) = ....

4.7

Jawaban terverifikasi