Pertanyaan

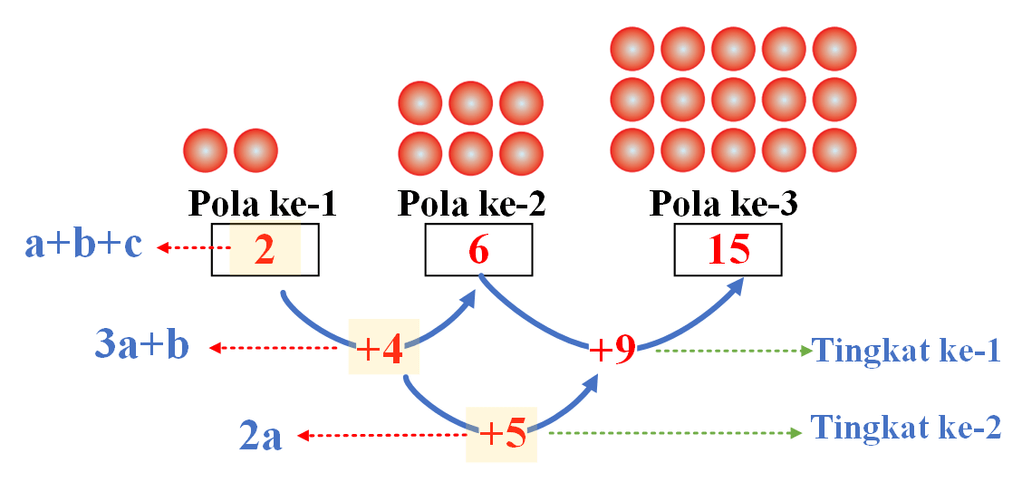
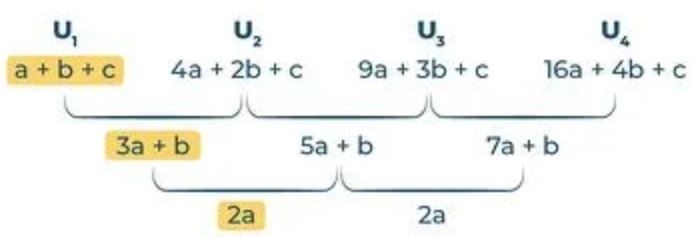
Tentukan banyak lingkaran pada pola ke-10, ke-100, ke- n pada pola berikut, untuk sebarang bilangan bulat positif.

Tentukan banyak lingkaran pada pola ke-10, ke-100, ke- $n$ pada pola berikut, untuk sebarang bilangan bulat positif.

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

F. Freelancer6

Master Teacher

Jawaban terverifikasi

Jawaban

banyak lingkaran pada pola ke 100 adalah 24.653buah

banyak lingkaran pada pola ke 100 adalah 24.653 buah

Pembahasan

Berdasarkan gambar pada soal, maka pola bilangan dapat dijabarkan sebagai berikut : Berdasarkan pola diatas, maka barisan tersebut merupakan barisan aritmetika bertingkat 2. Adapun rumus umum barisan aritmetika bertingkat sebagai berikut : Berdasarkan pola barisan bertingkat dua dari rumus (1), diperoleh pola barisan arimetika sebagai berikut : Pola barisan aritmetika tersebut bertujuan untuk memudahkan dalam mendapatkan nilai a, b, dan c yang terdapat pada rumus (1)barisan aritmatika bertingkat dua. Kemudiancari nilai a, b, dan c barisan padasoal dengan menyamakan pada rumus pola barisan aritmetika diatas : Berdasarkan gambar diatas maka : Setelah diperoleh nilai a=2,5;b= 3,5;dan c=3,substitusikan nilainya ke dalam rumus (1)barisan aritmatika bertingkat dua Dengan memperhatikan pola tersebut, maka dapat disimpulkan bahwa banyak bola padapola ke- , untuk bilangan bulat positif adalah Banyak lingkaran pada pola ke-10 : Jadi banyak lingkaran pada pola ke 10 adalah 218 buah Banyak lingkaran pada pola ke-100 : Jadi banyak lingkaran pada pola ke 100 adalah 24.653buah

Berdasarkan gambar pada soal, maka pola bilangan dapat dijabarkan sebagai berikut :

Berdasarkan pola diatas, maka barisan tersebut merupakan barisan aritmetika bertingkat 2. Adapun rumus umum barisan aritmetika bertingkat sebagai berikut :

Berdasarkan pola barisan bertingkat dua dari rumus (1), diperoleh pola barisan arimetika sebagai berikut :

Pola barisan aritmetika tersebut bertujuan untuk memudahkan dalam mendapatkan nilai a, b, dan c yang terdapat pada rumus (1) barisan aritmatika bertingkat dua.

Kemudian cari nilai a, b, dan c barisan pada soal dengan menyamakan pada rumus pola barisan aritmetika diatas :

Berdasarkan gambar diatas maka :

begin mathsize 14px style ring operator 2 straight a equals 5 space space space space space straight a equals 5 over 2 space space bold space bold space bold a bold equals bold 2 bold comma bold 5 end style

Setelah diperoleh nilai a=2,5; b=3,5; dan c=3,substitusikan nilainya ke dalam rumus (1) barisan aritmatika bertingkat dua

undefined

Dengan memperhatikan pola tersebut, maka dapat disimpulkan bahwa banyak bola pada pola ke-, untuk bilangan bulat positif adalah

Banyak lingkaran pada pola ke-10 :

Jadi banyak lingkaran pada pola ke 10 adalah 218 buah

Banyak lingkaran pada pola ke-100 :

Jadi banyak lingkaran pada pola ke 100 adalah 24.653 buah